| int |
M.dim1() |
returns n, the number of rows of M.
|
| int |
M.dim2() |
returns m, the number of columns of M.
|
| vector& |
M.row(int i) |
returns the i-th row of M (an m-vector).
Precondition
0 < = i < = n - 1.
|
| vector |
M.col(int i) |
returns the i-th column of M (an n-vector).
Precondition
0 < = i < = m - 1.
|
| matrix |
M.trans() |
returns MT (m x n - matrix).
|
| matrix |
M.inv() |
returns the inverse matrix of M.
Precondition M.det() 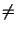 0. 0.
|
| double |
M.det() |
returns the determinant of M.
Precondition M is quadratic.
|
| vector |
M.solve(vector b) |
returns vector x with M*x = b.
Precondition M.dim1() == M.dim2() = =b.dim()
and M.det() ! = 0.
|
| double& |
M(int i, int j) |
returns Mi, j.
Precondition
0 < = i < = n - 1 and
0 < = j < = m - 1.
|
| matrix |
M + M1 |
Addition.
Precondition M.dim1() == M1.dim1() and M.dim2() == M1.dim2().
|
| matrix |
M - M1 |
Subtraction.
Precondition M.dim1() == M1.dim1() and
M.dim2() == M1.dim2().
|
| matrix |
M * M1 |
Multiplication.
Precondition M.dim2() == M1.dim1().
|
| vector |
M * vector vec |
Multiplication with vector.
Precondition M.dim2() == vec.dim().
|
| matrix |
M * double x |
Multiplication with double x.
|
| void |
M.print(ostream& O) |
prints M row by row to ostream O.
|
| void |
M.print() |
prints M cout.
|
| void |
M.read(istream& I) |
reads
M.dim1() x M.dim2() numbers from input stream
I and writes them row by row into matrix M.
|
| void |
M.read() |
prints M from cin.
|
| ostream& |
ostream& O << M |
writes matrix M row by row to the output stream O.
|
| istream& |
istream& I >> matrix& M |
reads a matrix row by row from the input stream I
and assigns it to M.
|
Be aware that the operations on vectors and matrices incur rounding error and
hence are not completely reliable. For example, if M is a matrix, b is a
vector, and x is computed by x = M.solve(b) it is not necessarly true that
the test b == M * b evaluates to true. The types integer_vector and integer_matrix provide exact linear algebra.