Maximum Flow ( max_flow )

Let G = (V, E) be a directed graph, let s and t be distinct vertices in G and let cap : E $\longrightarrow$ IR_{$\ge$ 0} be a non-negative function on the edges of G. For an edge e, we call cap(e) the capacity of e. An (s, t)-flow or simply flow is a function f : E $\longrightarrow$ IR_{$\ge$ 0} satisfying the capacity constraints and the flow conservation constraints:

$\begin{array}{lcl} (1) & 0\leq f(e)\leq cap(e) & \mbox{ for every edge } e\in ... ... v\in V\backslash \{\hspace{\setspacing}s,t\hspace{\setspacing} \} \end{array}$
The value of the flow in the net flow into t (equivalently, the net flow out of s). The net flow into t is the flow into t minus the flow out of t. A flow is maximum if its value is at least as large as the value of any other flow.

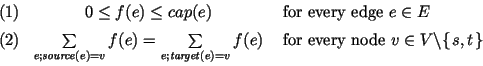
All max flow implementations are template functions. The template parameter NT can be instantiated with any number type. In order to use the template version of the function the files

#include <LEDA/graph_algs.h>
#include <LEDA/templates/max_flow.t>

must be included.

There are pre-instantiations for the number types int and double.The pre-instantiated versions have the same function names except for the suffix _T. In order to use them either

#include <LEDA/max_flow.h>

or

#include <LEDA/graph_alg.h>

has to be included (the latter file includes the former). The connection between template functions and pre-instantiated functions is discussed in detail in the section ``Templates for Network Algorithms'' of the LEDA book.

Special care should be taken when using the template functions with a number type NT that can incur rounding error, e.g., the type double. The section ``Algorithms on Weighted Graphs and Arithmetic Demand'' of the LEDA book contains a general discussion of this issue. The template functions are only guaranteed to perform correctly if all arithmetic performed is without rounding error. This is the case if all numerical values in the input are integers (albeit stored as a number of type NT) and if none of the intermediate results exceeds the maximal integer representable by the number type ( 2⁵³ - 1 in the case of doubles). All intermediate results are sums and differences of input values, in particular, the algorithms do not use divisions and multiplications.

The algorithms have the following arithmetic demands. Let C be the maximal absolute value of any edge capacity. If all capacities are integral then all intermediate values are bounded by d*C, where d is the out-degree of the source.

The pre-instantiations for number type double compute the optimal matching for a modified capacity function cap1, where for every edge e

$\mathit{cap1}[e]= \mathit{sign}(\mathit{cap}[e]) \lfloor \Vert \mathit{cap}[\mathit{e}] \Vert * S \rfloor / S$
and S is the largest power of two such that S < 2⁵³/(d*C).

The value of the maximum flow for the modified capacity function and the value of the maximum flow for the original capacity function differ by at most m*d*C*2^-52.

The following functions are available:

NT	MAX_FLOW_T(graph G, node s, node t, edge_array<NT> cap, edge_array<NT>& f)
		computes a maximum (s, t)-flow f in the network (G, s, t, cap) and returns the value of the flow. The implementation uses the preflow-push method of Goldberg and Tarjan [] with the local and global relabeling heuristic and the gap heuristic. The highest level rule is used to select active nodes. The section on maximum flow of the LEDA book gives full information.
NT	MAX_FLOW_T(graph G, node s, node t, edge_array<NT> cap, edge_array<NT>& f, int& num_pushes, int& num_edge_inspections, int& num_relabels, int& num_global_relabels, int& num_gaps, float h)
		as above; The additional parameter report some statistics of the execution (the number of pushes, the number of edge inspections, the number of relabels, the number of global relabels, and the number of nodes moved by the gap heuristic. The parameter h controls the global relabeling heuristic. The global relabeling heuristic is called every h*m edge inspections. The choice h = 5 seems reasonable.
bool	CHECK_MAX_FLOW_T(graph G, node s, node t, edge_array<NT> cap, edge_array<NT> f)
		checks whether f is a maximum flow in the network (G, s, t, cap). The functions returns false if this is not the case.
bool	MAX_FLOW_SCALE_CAPS(graph G, node s, edge_array<double>& cap)
		replaces cap[e] by cap1[e] for every edge e, where cap1[e] is as defined above. The function returns false if the scaling changed some capacity, and returns true otherwise.

The following functions are only available in template form. They allow to study the effect of different heuristics and of different selection rules on the preflow push method. The class SET must provide the following operations: construction, destruction, del, insert, insert0, and clear; see the LEDA book for details. Three implementations are part of the distribution: fifo_set, hl_set, and mfifo_set.

NT	MAX_FLOW_BASIC_T(graph G, node s, node t, edge_array<NT> cap, edge_array<NT>& flow, SET& U, int& num_pushes, int& num_edge_inspections, int& num_relabels)
		The basic version of the preflow push algorithm: No heuristic is used.
NT	MAX_FLOW_LH_T(graph G, node s, node t, edge_array<NT> cap, edge_array<NT>& flow, SET& U, int& num_pushes, int& num_edge_inspections, int& num_relabels)
		The preflow push method with the distinction between low and high nodes.
NT	MAX_FLOW_LRH_T(graph G, node s, node t, edge_array<NT> cap, edge_array<NT>& flow, SET& U, int& num_pushes, int& num_edge_inspections, int& num_relabels)
		The preflow push method with the distinction between low and high nodes and the local relabeling heuristic.
NT	MAX_FLOW_GRH_T(graph G, node s, node t, edge_array<NT> cap, edge_array<NT>& flow, SET& U, int& num_pushes, int& num_edge_inspections, int& num_relabels, int& num_global_relabels, float h)
		The preflow push method with the distinction between low and high nodes, the local relabeling heuristic, the global relabeling heuristic, and the two-phase approach. The global relabeling heuristic is applied every h*m edge inspections.
NT	MAX_FLOW_GAP_T(graph G, node s, node t, edge_array<NT> cap, edge_array<NT>& flow, SET& U, int& num_pushes, int& num_edge_inspections, int& num_relabels, int& num_global_relabels, int& num_gaps, float h)
		The preflow push method with the distinction between low and high nodes, the local relabeling heuristic, the global relabeling heuristic, the two-phase approach, and the gap heuristic. The global relabeling heuristic is applied every h*m edge inspections.

The following generators can be used to generate max-flow problems with integer capacities. The generators return a GRAPH<int,int> G and nodes s and t. The edge capacities are available as edge data, i.e., the capacity of edge e is available as G[e] and the edge array of capacities is passed as G.edge_data(). For detailed information about the generators we refer to the LEDA book.

void	max_flow_gen_rand(GRAPH<int,int>& G, node& s, node& t, int n, int m)
		A random graph with n nodes, m edges, and random edge capacities in [2,11] for the edges out of s and in [1,10] for all other edges.
void	max_flow_gen_CG1(GRAPH<int,int>& G, node& s, node& t, int n)
		A generator suggested by Cherkassky and Goldberg.
void	max_flow_gen_CG2(GRAPH<int,int>& G, node& s, node& t, int n)
		Another generator suggested by Cherkassky and Goldberg.
void	max_flow_gen_AMO(GRAPH<int,int>& G, node& s, node& t, int n)
		A generator suggested by Ahuja, Magnanti, and Orlin.