Rational Points ( rat_point )

Definition

An instance of data type rat_point is a point with rational coordinates in the two-dimensional plane. A point with cartesian coordinates (a, b) is represented by homogeneous coordinates (x, y, w) of arbitrary length integers (see Integers of Arbitrary Length) such that a = x/w and b = y/w and w > 0.

#include < LEDA/rat _point.h >

Types

rat_point::coord_type	the coordinate type (rational).
rat_point::point_type	the point type (rat_point).
rat_point::float_type	the corresponding floating-point type (point).

Creation

rat_point	p	introduces a variable p of type rat_point initialized to the point (0, 0).
rat_point	p(rational a, rational b)	introduces a variable p of type rat_point initialized to the point (a, b).
rat_point	p(int a, int b)	introduces a variable p of type rat_point initialized to the point (a, b).
rat_point	p(integer x, integer y, integer w)
		introduces a variable p of type rat_point initialized to the point with homogeneous coordinates (x, y, w) if w > 0 and to point (- x, - y, - w) if w < 0. Precondition w $\not=$ 0.
rat_point	p(rat_vector v)	introduces a variable p of type rat_point initialized to the point (v[0], v[1]). Precondition: v.dim() = 2.
rat_point	p(point p, int prec = rat_point::default_precision)
		introduces a variable p of type rat_point initialized to the point with homogeneous coordinates ($\lfloor$P*x$\rfloor$,$\lfloor$P*x$\rfloor$, P), where p = (x, y) and P = 2prec. If prec is non-positive, the conversion is without loss of precision, i.e., prec is chosen as a sufficiently large power of two such that P*x and P*y are integers.

Operations

point	p.to_float()	returns a floating point approximation of p.
rat_vector	p.to_vector()	returns the vector extending from the origin to p.
integer	p.X()	returns the first homogeneous coordinate of p.
integer	p.Y()	returns the second homogeneous coordinate of p.
integer	p.W()	returns the third homogeneous coordinate of p.
double	p.XD()	returns a floating point approximation of p.X().
double	p.YD()	returns a floating point approximation of p.Y().
double	p.WD()	returns a floating point approximation of p.W().
rational	p.xcoord()	returns the x-coordinate of p.
rational	p.ycoord()	returns the y-coordinate of p.
double	p.xcoordD()	returns a floating point approximation of p.xcoord().
double	p.ycoordD()	returns a floating point approximation of p.ycoord().
rat_point	p.rotate90(rat_point q)	returns p rotated by 90 degrees about q.
rat_point	p.rotate90()	returns p rotated by 90 degrees about the origin.
rat_point	p.reflect(rat_point p, rat_point q)
		returns p reflected across the straight line passing through p and q. Precondition p $\not=$q.
rat_point	p.reflect(rat_point q)	returns p reflected across point q.
rat_point	p.translate(rational dx, rational dy)
		returns p translated by vector (dx, dy).
rat_point	p.translate(integer dx, integer dy, integer dw)
		returns p translated by vector (dx/dw, dy/dw).
rat_point	p.translate(rat_vector v)	returns p + v, i.e., p translated by vector v. Precondition v.dim() = 2.
rat_point	p + rat_vector v	returns p translated by vector v.
rat_point	p - rat_vector v	returns p translated by vector - v.
rational	p.sqr_dist(rat_point q)	returns the squared distance between p and q.
int	p.cmp_dist(rat_point q, rat_point r)
		returns compare(p.sqr$\_$dist(q), p.sqr$\_$dist(r)).
rational	p.xdist(rat_point q)	returns the horizontal distance between p and q.
rational	p.ydist(rat_point q)	returns the vertical distance between p and q.
rat_vector	p - q	returns the difference vector of the coordinates.
ostream&	ostream& O << p	writes the homogeneous coordinates (x, y, w) of p to output stream O.
istream&	istream& I >> rat_point& p
		reads the homogeneous coordinates (x, y, w) of p from input stream I.

Non-Member Functions

int	orientation(rat_point a, rat_point b, rat_point c)
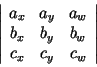
		computes the orientation of points a, b, c as the sign of the determinant $\left\vert\begin{array}{ccc} a_x & a_y & a_w\\ b_x & b_y & b_w\\ c_x & c_y & c_w \end{array} \right\vert$ i.e., it returns +1 if point c lies left of the directed line through a and b, 0 if a,b, and c are collinear, and -1 otherwise.
int	cmp_signed_dist(rat_point a, rat_point b, rat_point c, rat_point d)
		compares (signed) distances of c and d to the straight line passing through a and b (directed from a to b). Returns +1 (-1)if c has larger (smaller) distance than d and 0 if distances are equal.
int	cmp_distances(rat_point p1, rat_point p2, rat_point p3, rat_point p4)
		compares the distances (p1,p2) and (p3,p4). Returns +1 (-1) if distance (p1,p2) is larger (smaller) than distance (p3,p4), otherwise 0.
rat_point	midpoint(rat_point a, rat_point b)
		returns the midpoint of a and b.
rational	area(rat_point a, rat_point b, rat_point c)
		computes the signed area of the triangle determined by a,b,c, positive if orientation(a, b, c) > 0 and negative otherwise.
bool	collinear(rat_point a, rat_point b, rat_point c)
		returns true if points a, b, c are collinear, i.e., orientation(a, b, c) = 0, and false otherwise.
bool	right_turn(rat_point a, rat_point b, rat_point c)
		returns true if points a, b, c form a righ turn, i.e., orientation(a, b, c) < 0, and false otherwise.
bool	left_turn(rat_point a, rat_point b, rat_point c)
		returns true if points a, b, c form a left turn, i.e., orientation(a, b, c) > 0, and false otherwise.
int	side_of_halfspace(rat_point a, rat_point b, rat_point c)
		returns the sign of the scalar product (b - a)*(c - a). If b $\not=$a this amounts to: Let h be the open halfspace orthogonal to the vector b - a, containing b, and having a in its boundary. Returns +1 if c is contained in h, returns 0 is c lies on the the boundary of h, and returns -1 is c is contained in the interior of the complement of h.
int	side_of_circle(rat_point a, rat_point b, rat_point c, rat_point d)
		returns +1 if point d lies left of the directed circle through points a, b, and c, 0 if a,b,c,and d are cocircular, and -1 otherwise.
bool	incircle(rat_point a, rat_point b, rat_point c, rat_point d)
		returns true if point d lies in the interior of the circle through points a, b, and c, and false otherwise.
bool	outcircle(rat_point a, rat_point b, rat_point c, rat_point d)
		returns true if point d lies outside of the circle through points a, b, and c, and false otherwise.
bool	on_circle(rat_point a, rat_point b, rat_point c, rat_point d)
		returns true if points a, b, c, and d are corcircular.
bool	cocircular(rat_point a, rat_point b, rat_point c, rat_point d)
		returns true if points a, b, c, and d are corcircular.
bool	affinely_independent(array<rat_point> A)
		decides whether the points in A are affinely independent.
bool	contained_in_simplex(array<rat_point> A, rat_point p)
		determines whether p is contained in the simplex spanned by the points in A. A may consists of up to 3 points. Precondition The points in A are affinely independent.
bool	contained_in_affine_hull(array<rat_point> A, rat_point p)
		determines whether p is contained in the affine hull of the points in A.