My research follows the general philosophy and studies
algorithms/data structures with applications in wireless ad hoc communication and sensor
networks. An ad hoc network is a network on a set of autonomous wireless nodes. There is no fixed
infrastructure nor central server. All the nodes act as routers to discover and maintain routes to other nodes. The nodes in the
network can be changing dynamically (turned on/off arbitrarily) and can be moving continuously. The wireless nodes are normally
energy-constrained and have a fixed transmission range, e.g., a unit disk. Such a network can be modeled by a unit-disk graph such
that there is an edge on every pair of nodes within distance 1. When the nodes move, the underlying topology of the network
changes constantly. Therefore, the algorithms and data structures that are suitable for wireless mobile networks must be
local, lightweight, flexible, and stable. A localized and lightweight structure is desirable for the reason of
scalability. The structures have to be flexible since the topology of the wireless nodes can be arbitrary and most of the time not
controllable. Furthermore, we want a stable structure that doesn't change too many times as the nodes are inserted/deleted or moving
around. We also prefer structures that can be updated incrementally rather than rebuilt from scratch. I will illustrate
this idea by giving examples as follows. Besides the rigorous theoretical analysis of the structures, their good performance in
practice was also validated by implementations and simulations.
Discrete mobile centers [9] The discrete centers in a mobile ad hoc network are a subset of nodes
so that any node can communicate with at least one center directly at any time. This is a very fundamental problem with numerous
applications in building hierarchical structures or routing backbones. We proposed an algorithm that generates stable centers
of good quality. The number of centers is at most a constant times the minimum number possible. Also, the minimum number of changes
of the centers is bounded by a log log factor of the minimum number of changes of
any discrete centers with a constant approximation ratio. We show that the discrete centers are
efficient, local, responsive and compact. Furthermore, they can be constructed in a localized and distributed manner, which makes
them appropriate for mobile networking scenarios.
Video clips: Random points (25MB), Clustered points [15Mb], Clustered points by both location and velocity information [8Mb]
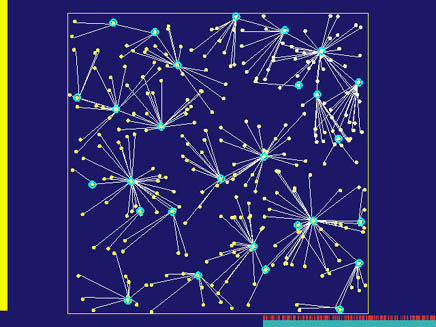
Figure 1: Discrete mobile centers on random points. The discrete centers are nodes with blue annuli. The white edges connect discrete centers with their clients.
Spanner backbone routing graph [8] The density of the discrete centers, i.e., the maximum number of centers inside any unit disk, is bounded by a constant. This property is used in constructing a linear-size ``backbone'' subgraph in the mobile wireless network so that both the number of hops and the Euclidean length of the shortest path on the backbone graph are at most a constant times those in the original graph. This subgraph enjoys another property that no two edges are crossing each other and therefore can be used in the perimeter routing to bypass the ``local minimum'' in a greedy geographic routing scheme [5][17].
Video clips: Restricted Delaunay graph under motion [50Mb]
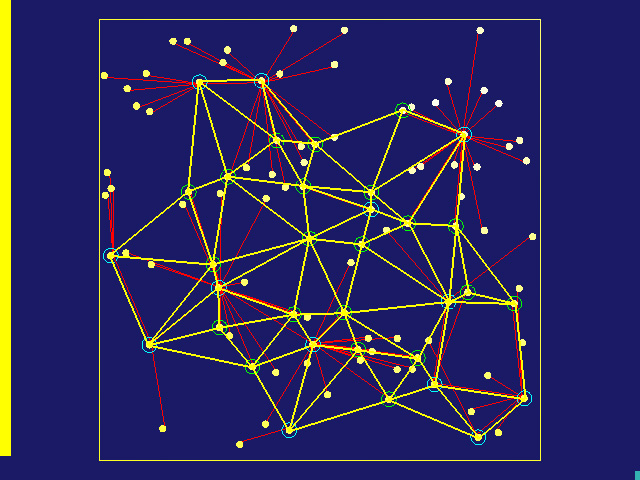
Figure 2: Spanner backbone routing graph. The yellow edges are the Restricted Delaunay Graph. The red edges are the edges connecting discrete centers with the clients.
Locating and bypassing routing holes [6] The fundamental difficulty greedy geographic
routing strategies [5][17] face: the ``local minimum phenomenon'' that can cause packets to get stuck
was restudied in depth. The ``stuck nodes'' where packets may get stuck in greedy forwarding were rigorously defined and can be
identified by a local Tent rule. We also design a
distributed algorithm, BoundHole, to build the routes
around routing holes and help the messages get out of stuck nodes. These hole-surrounding routes can be used in many applications
like geographic routing, path migration, information storage mechanisms, disaster recovery, etc.
กก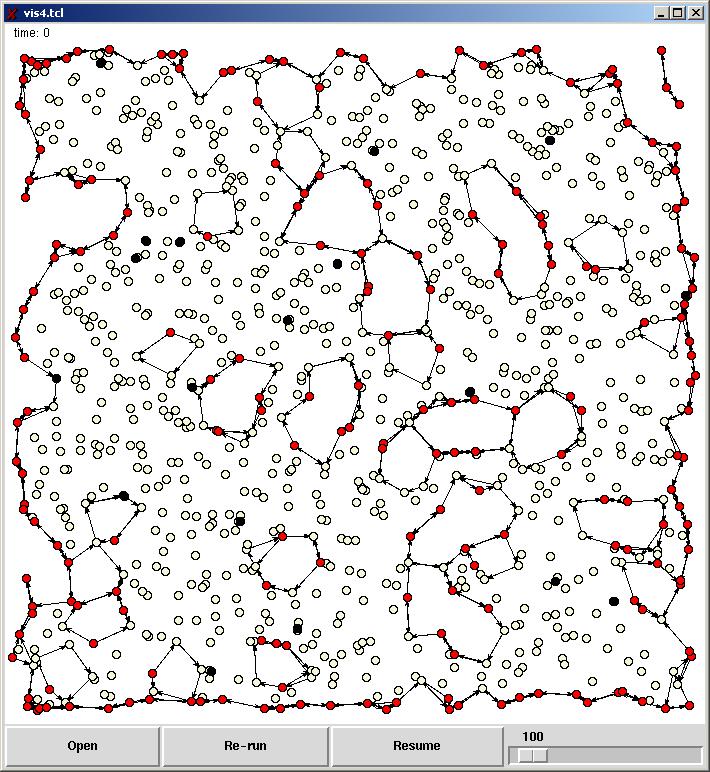
Figure 3: Stuck nodes and routing holes. The red nodes are the stuck nodes where packets might be stuck at a local minimum in a greedy geographic forwarding scheme. The black nodes are failed nodes due to energy depletion. Each stuck node is on a routing hole identified by the algorithm BoundHole.
Load balanced routing [12][14] There are two goals that people want to achieve on routing in general: load balancing, i.e., no
node is highly congested and low delay, i.e., the routing path is as short as possible. The load
balancing competitive ratio and stretch factor, represent how well we can achieve the two goals respectively.
In general, these two goals are conflicting with each other. But when the wireless nodes
are distributed on a line or in a narrow band, we show by an algorithm that both constant load balancing ratio and constant
stretch factor can be obtained at the same time [14]. The algorithm is distributed and memory efficient. And it admits
efficient implementation and update schemes. When the nodes are distributed in the plane, we show a non-trivial
tradeoff of the two factors in terms of the density of the nodes. Specifically, when the maximum number of points inside a unit disk
is 
, the optimal algorithm by using only paths with stretch
factor no more than c generates the maximum load on the nodes at most 
times that of the optimal algorithm without path length restriction [12].
Approximate medians/centerpoints [2][3] The discrete centers problem fixes the sizes of the clusters and minimizes the number of
clusters in total. A dual problem is to fix the number of clusters and find the centers that minimize the sizes of the clusters. In
other words, we try to find a point such that any line passing through it should partition the points in parts
of roughly half the size. This notion is formalized as the median in 1D and the centerpoint in
2D. As maintenance of the exact median and centerpoint under motion is very expensive, we study
their approximations which are much more stable [2]. Besides the application in mobile
networks where the centerpoint is the ideal position of the wireless mobile base station, the approximate
median/centerpoint finds additional applications in temporal databases. For example,
we can construct efficient range searching structures of moving points by finding the medians recursively in a divide-and-conquer
manner [3].
Well-separated pair decomposition for unit-disk graph metric [13] What we have discussed so far is
more or less clustering the points. We can also cluster the pair-wise distances, i.e., represent the quadratic number of pairwise distances of the nodes by a linear size structure by
losing only a small factor in approximation. For example, we can represent the shortest path distances of all the pairs in a unit
disk graph by an almost linear-size data structure called the well-separated pair decomposition (WSPD). A
(1+
)-well separated pair is a pair of sets, blue point set and red point
set, so that the shortest path distance between any blue/red pair doesn't differ by a factor
(1+), for any >0, thus can
be approximated by any blue/red pair. A well-separated pair decomposition is simply a set of well separated pairs that
``cover'' all pairs of points. We show that a WSPD with an almost linear number of pairs can be
computed in almost linear time. This result finds a lot of applications in computing approximate
(bichromatic) nearest/furthest pair, diameter, median, minimum spanning/steiner
tree etc., since almost every problem involving computing all pairs distances can be approximately answered by using the WSPD
and saving computing time and space.
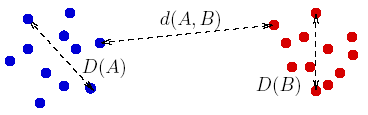
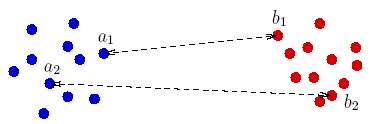
Figure 4: A well-separated pair
of blue points and red points. The distance between any two pairs of blue/red
points doesn't differ by a factor
(1+).
Kinetic spanners [10][11] Another way to represent all pairs distances of
n points is to construct a linear size graph such that the shortest path distance of any pair of points on the
graph is at most a factor (1+)
of the original metric distance, for any
>0. Such a graph is called a (1+)-spanner. We study points in
Rd and construct a (1+)-spanner with a linear number of edges. The
advantage of our spanner, to be distinguished from all the spanners proposed previously, is that it can be adapted easily
under motion. This property is essential since the numerous applications of a spanner now can be transferred to the moving
domain. For example, in protein modeling, the proximity information captured by the spanner is closely related to the
interaction forces between the molecules; in physical simulation, we can predict the collision or self-collision by inspecting the
spanner edges only. As a bonus feature, the spanner implies a (1+)-WSPD and an
8-approximate k-center, for any given k. This is the first time we know how to maintain WSPD and an
approximate k-center for moving points. We can also show that the spanner can be defined in a similar way on points in a metric
with doubling dimension [15] where a ball can be covered by at most a constant number of balls of half radii. Since
the peer-to-peer networks usually admit metrics with doubling dimension [16], the spanner gives a structured
overlay network which approximates the underlying network topology and has efficient routing and dynamic update
schemes [10].
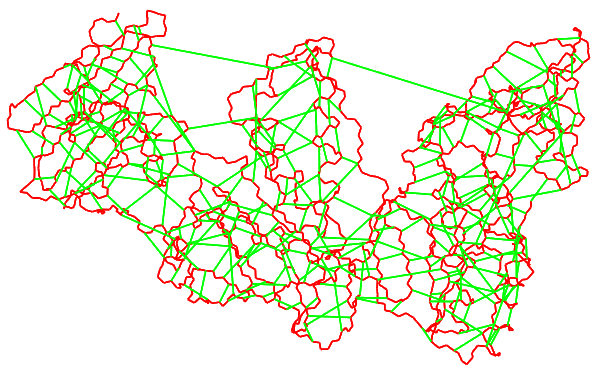
Figure 5: A spanner on a protein backbone. The spanner consists of the backbone edges (red) and a number of additional edges, the shortcuts (green). There is a path between any two backbone atoms with length at most 3 times their Euclidean distance.
Range searching in sensor networks Geometric range searching has been extensively studied in computational
geometry [1]. Objects are preprocessed into a data structure such that queries about the objects inside a geometric
range can be answered efficiently. While sensor networks are viewed as a distributed database where each sensor has a sampled
value of a hidden continuous measure field, the underlying communication network introduces difficulty of applying the
geometric range searching. Furthermore, it's desirable to have a distributed and memory efficient storage/retrieval scheme rather
than some fixed global data structures. In a word, the central question is ``who stores what''.
In [7], we proposed a scheme where a node knows a ``fraction'' of the information from distant parts of the network in an exponentially
decaying fashion by distance. The fractionally cascaded information exploits locality that has not been addressed before,
and at the same time keeps a summarized view of far away regions. We have a storage scheme and a range query algorithm such that
each sensor saves O(log n) amount of information and the worst case communication cost to answer a range query is close to the
optimum.
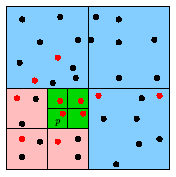
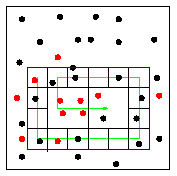
Figure 6: Range searching in sensor networks. The left figures shows a point p's view of the world. The right figures shows how the information is collected by touring the query range.
In conclusion, the localized, lightweight, flexible and stable structures and algorithms are especially interesting from a philosophical point of view. In the algorithm design field, we have always been looking at the world from top down. Here we are proposing a distributed and ``bottom-up'' type of view. The data structures I have been discussing all share the same flavor and illustrate how globally optimal behaviors and structures ``emerge'' from the simple local interactions -- the exact philosophy of many complex systems in nature like the biological system or the social system. Indeed, it's exciting to see that the algorithms can be applied to a large range of problems from mobile networking to robotics to protein folding. Controlled by simple local rules, the structures exhibit complicated behaviors and evolve by themselves. Besides the significance and necessity of better understanding of how the behaviors emerge, the study of data structures and distributed algorithms along this line will find applications in many other complex systems as well.