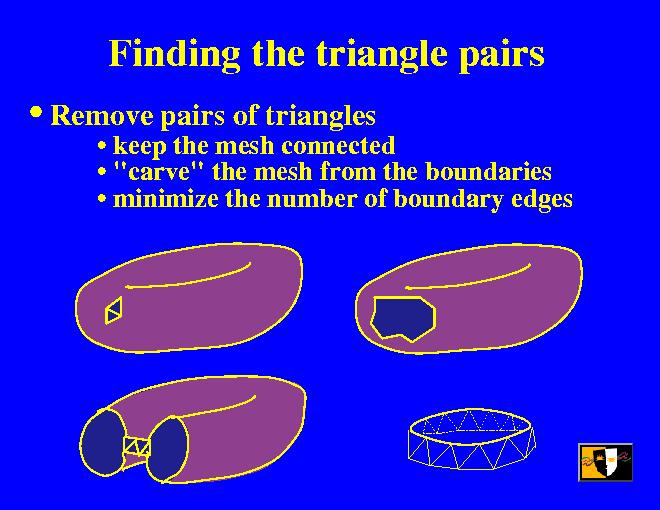
Earlier I said that we want to partition the full control mesh into pairs of adjacent triangles. We want to do this pairing fast, and we want to minimize the number of triangles that cannot find a unique pair.
The only way that we are going to end up with unpaired triangles is if we separate the mesh into disjoint parts, so we want to avoid doing that. If we try to keep the mesh as compact as possible by carving evenly from the boundaries, we have fewer chances of breaking the mesh. Trying to minimize the number of boundary edges automatically keeps the mesh compact.
This series of images shows the general flavor how the algorithm proceeds. First we randomly remove a pair of triangles, creating a boundary. Then we start carving away at the boundary. We continue carving, and since we avoid breaking things apart, we may in this case end up with a ring of triangles. At some stage we have to break this ring, and the remaining triangles can then be paired starting from the ends.