We wish to model and animate an underwater scene containing (hopefully multiple) jellyfish. Light scattering through the thin tissue layers of a jellyfish causes beautiful effects that have been captured by marine photographers (and visitors to the Monterey Bay aquarium), as shown in the photos below. Reproducing these images on a computer seems challanging due to the difficulty in modeling both the intricate detail of the jellyfish's geometry as well as modeling the light scattering properties of jellyfish tissue. Additionally, "plausible" animation of jellyfish movement will need to be created.

Photo credit: Crystal Fong & Jonathan Hui (from the Monterey Bay Aquarium)

In addition to modeling light scattered by the Jellyfish, we hope to capture the volumetric scattering properties of the water medium itself. The picture below shows light scattering near the water's surface, as well as the optical manhole effect due to total internal refraction as discussed in class. Ideally, we will be able to render both of these effects in our scenes.

(Kayvon will be working on this part of the project)

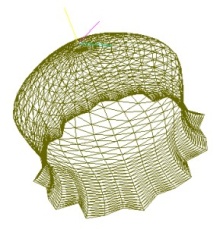
The jellyfish we are attempting to model has three primary features. (1) A large pulsating bell, (2) Long string-like tentacles hanging down from the end of the bell, and (3) larger, "squiggly" tentacles that extend down from the jellyfish's organs down from the center of the bell.

Modeling the Bell: We assume radial symmetry of the bell structure, and use the rotation about a directional axis of a curve defined by a Hermite spline to generate a mesh (Catmull-Rom splines were intitially used, however to precisely model the bell we found that the ability to specify tangents at the control points was necessary). Additionally, to create the ruffles apparent in the lower parts of the bell, we perturb the radial distance of the surface from the axis with a sine function on the radial angle phi. The magnitude of this perturbation is modulated by an additional Hermite spline that varies from the top to the bottom of the bell. We plan on generating a triangle mesh from this parameterization, and using the triangle mesh for rendering in PBRT. A PBRT shape has already been created to perform this step.

While physical sim will be used to animate the tentacles, we will use keyframe animation to animate the bell. An the keyframe splines to produce the animation of a pulsing bell shape is given below.

Modeling the Small Tentacles: We plan on modeling tentacles as generalized cylinders. A Catmull-Rom spline will define the backbone spline of the tentacle, and a second Catmull-Rom spline will specify variation magnitude of the radius over the length of the tenacle. The control pts for the backbone spline will be obtained via simple mass-spring simulation of a small number of particles. We hope a simple midpoint integrator will be able to produce reasonably results.

Modeling the Central Tentacles: The jellyfish has three large tentacles that feature complicated geometry. We observe these tentacles have a shape that is more like a ribbon than a generalized cylinder. One edge of the tentacle has fairly low curvature while curvature on the other edge is extremely high. Again, we intend to model the curvature of both edges via Catmull-Rom spline curves, however remain unsure how to best generate control points for the high-curvature edge. Thusfar we have utilized an algorithm based on a random walk, but are currently investigating rejection sampling or fractal-curve based methods. We intend to animate the central tentacles via physical simulation as well. It is unclear whether the simulation will need to treat the tentacle as a thin sheet, or if a mass-spring rope model will be sufficient.

(Tim's is in charge of this part of the project, Kayvon will help as soon as the geometric modeling and animation is done)

In order to render the underwater scenes we will simulate two different light-scattering phenomena. (1) The scattering of light through thin surfaces such as the jellyfish tentacles and the outer layer of the bell, and (2) Scattering of caustic light through participating media such as water and the internal organs of the jellyfish.

Scattering of Light Through Thin Surfaces: Many structures in the jellyfish, including the tentacles and the outer layer of the bell consist of a thin surface of biological tissue. The apparent opacity of these surfaces varies greatly with viewing angle, as the optical depth increases for grazing angles of incidence and exit. The appearance of these surfaces also seems to derive mostly from in-scattering of light, rather than from surface reflections.

In order the simulate these effects we will implement the model in "Reflection from Layered Surfaces due to Subsurface Scattering" (Hanrahan and Krueger, 1993). This paper decomposes the exit radiance from a point on a thin surface into four terms. Surface reflectance and specular transmission comprise the parts of the BRDF and BTDF that do not depend on in-scattering. The two remaining terms account for in-scattered light from both the near and far sides of the surface.

We will assume that the jellyfish surfaces are sufficiently thin that multiple scattering events can be ignored and the incident and exit points for rays scattered by the surface can be treated as coincident, and will also assume that the surface tissue can be accurately modeled with a Heyney-Greenstein phase function. Under these assumptions the above paper provides a closed-form solution for the amount of in-scattered radiance from the near and far sides of the surfaces as a function of surface thickness. The formulation given assumes planar surfaces, where the effective thickness is a function of cos(wi) and cos(wo) (with wi and wo the incident and exit directions, respectively). However, we may have to extend this model to account for the significant curvature of the jellyfish surfaces.

Scattering of Caustic Light Through Participating Media: We intend to simulate the effects of skylight refracted by the ocean surface (caustic light) scattering in the ocean water, and possibly in the organs of the jellyfish. PBRT includes a volume integrator that can generate images with single scattering of light by participating media. In calculating their scattering solution, however, they consider only direct rays from light sources in the scene. This means that caustic light will never be scattered (only attenuated) by participating media. Similarly, although the photon mapping surface integrator can produce high-quality caustic lighting effects on surfaces in the scene, the photon mapper does not consider volumetric scattering events when calculating its solution.

To address this limitation we will implement the technique detailed in "Efficient Simulation of Light Transport in Scenes with Participating Media using Photon Maps" (Wann Jensen and Christensen, 1998). This technique takes advantage of the fact that photon maps are decoupled from the surface representation of the scene and can store photons at arbitrary coordinates, to simulate multiple volume scattering, volume caustics and color bleeding between volumes and surfaces. We will implement our solution as a coupled surface integrator/volume integrator pair. The two integrators will utilize a common photon map structure so that the precomputation cost of shooting photons can be shared.