You'll need to use this form of the equation for sampling the surface microfacet distribution function.
The purpose of this assignment is to add Monte Carlo sampling to lrt. When you finish the assignment, you will be able to specify integration for a surface in one of three ways:
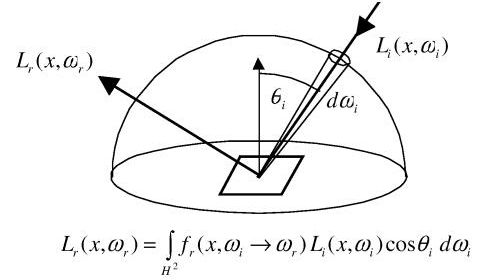
Remember from class the basic reflection (or scattering) equation:

You'll need to use this form of the equation for sampling the surface
microfacet distribution function.
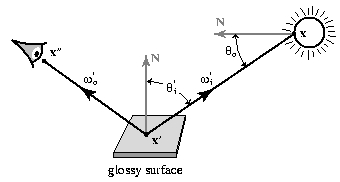
Another useful form of this function is the three-point form of the
equation (also talked about in class):
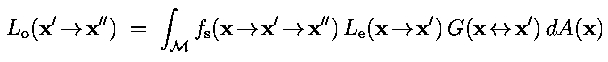
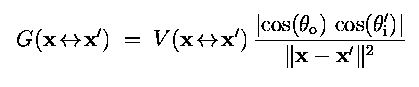
This is the same as the original reflectance equation, only we've
changed variables to integrate over area just the area of the light
source. Remember that V(x->x') is the visibility term. This is the
equation you'll need to use for performing your calculations based on
randomly sampling the light source.
Note that like other assignments, it is possible that we will update the lrt release before the assignment is due. Be sure to update your files if we announce a new release is out.
The first thing you should implement is the area light sources. You are asked to implement disk and triangle area lights. They are assumed to be diffuse emitters. You have to figure out how to generate uniform random samples on these shapes (with respect to area) given two uniform random numbers. You also have to be able to return a probability density function (pdf) for a given ray.
What to watch out for: sampling the light uniformly in area. As an example, think about the disk light source. Given two random numbers, u1 and u2, a random sample on the disk is not simply u1*radius, u2*theta. This will cluster the samples too close to the center of the disk.
After getting the area lights done, you should be able to code the integrator to handle the case of evaluating a surface color based on sampling the area light source. If you do this right, you should be able to render a scene that has diffuse surfaces (implemented for you) or Blinn glossy surfaces, multiple area lights, and some blockers to produce something with soft shadows.
What to watch out for: Check to see what the fr() routine does to make sure you provide it the correct values.
You should then implement sampling of glossy surfaces using the Blinn microfacet distribution function. We know from class this is (N dot H)^k. You will have to generate a random H vector based on the Blinn distribution, then reflect your ray about this H to generate your light vector. You'll also have to come up with a pdf for a point on the surface.
What to watch out for: Make sure your microfacet distribution function is normalized, as was derived in class. Also, generating a random H is not trivial. You first should generate an H value in the plane with the eye and surface normal. Then rotate it a random amount about the surface normal to produce your final H used in the calculations.
After doing the Blinn surface, you should add the appropriate code to the integrator and check to make sure everything works. You'll know it is working if you can get some shiny surfaces.
The last part of the assignment is to get multiple importance sampling to work. You have to have the area lights and the Blinn glossy surfaces working correctly to do this part. This part adds the last bit of code to your integrator. Essentially this code will make use of the sampling and pdf functions you've written, and will make better decisions about what to do with each sample it is given.
| Sampling Method | ||
|---|---|---|
| Light Source | BRDF | Combination |

| 
| 
|

| 
| 
|
Remember, these images are provided for reference, not as debugging tools. I may need to update these as I debug my software for the project. Your images should look very close to these, but they depend on how you choose to multi-sample your BRDF (I used 1 sample per pixel sample), and how you choose to do your multiple importance sampling (I chose the balance heuristic).
And, in case you're wondering, here's the same file rendered using a glossy surface sampling the light. I've turned up the light source intensity, and set it to be a shiny metal surface with roughness of 0.2. This one doesn't have the PI correction factor mentioned in the email either. But, you get the idea. Increasing the roughness will make the shiny patch larger and larger.

Another sample rib and its image, courtesy of Gulli Briem.
Copyright © 2000 Pat Hanrahan