Nonlinear Raytracing: Mirages Gaurav Garg Niloy J. Mitra

Introduction:

The aim of this project was to make a non-linear ray tracer for rays moving in non-constant medium(for details check our project proposal). The main reason behind such perception is the fact that our brain assumes light travelling in straight lines even when its actually following a curved path.

In the first part of the project, we implemented a voxel based ray tracer which basically models the nonlinear effects using piecewise linear segments. Refraction and total internal reflection were considered only at the faces of the voxels. Refractive Index(RI) was assumed to be constant inside each voxel. Refractive index variations were modelled to render the different phenomenon usually observed in nature due to nonlinear ray paths.

In the second part, we derived an analytical expression for the path traced by a ray given the refractive index as a function of space. We solved this differential equation under a specific model of variation of the refractive index(namely linearly with height) and used it for speeding up our non-linear ray tracer(in most cases we got speed up of a factor of 2-3).

Results:

All the images use a similar model. The horizontal plane is a texture mapped heightfield. The heightfield is enclosed by a cylinder which also has texture mapped to its inside surface. There is a also a point light source.

AVI Sequences:

Below are some of the effects we rendered which are best viewed as animated sequence(click on the images to run).

This beautiful animation was rendered to show how something which looked like a water body at a distance when we see it at a grazing angle, disappears as we move up. This is a common trick to differentiate between an oasis and a mirage.

This is another animation that shows a similar effect in which we move closer and down at the same time. The mirage becomes more pronounced as we start approaching grazing angles.

This sequence tries to model the shimmering effect in mirages that we see commmonplace on a hot day. The effect is due to local variations in the refractive index which we model by randomly perturbing the RI at different points.(In practice, the effect is more subtle and slower in nature, but we amplified it because we have only a few frames).

Some more cases:

In this case, we show a effect commonly known as towering. This is phenomenon by which common objects appears stretched/squashed due to non-constant RI. Such processes are observable in nature particularly during sunrise/sunset.

	Constant RI		RI Increases(linearly) with height		RI Decreases(linearly) with height

The series tries to model the phenomenon when utility poles appear to become submerged in water with increasing distance from the observer. The effect is caused by the two-image inferior mirage. Note here our horizon is very clearly defined and hence the submerging effect is not very convincing. However, the elongation of poles is aparrent at a distance.

	Constant RI		RI Increases(linearly) with height		RI Decreases(linearly) with height

These images were rendered to show which part of the plane and the cylinder gets wraped due to bending of light. Notice that as refractive index(RI) increases with height the textures on the plane seems to move forward while it moves backwards if the RI varies the other way. Internal reflection is also observed(middle two images). Note in the third image from the left, we get an effect similar to superior mirages due to which we can see the green strip(extreme top-right) which is not visible with constant RI. Further, since this image has higher RI gradient we see more internal reflection. Finally, we need smaller voxel size, else we get minor artifacts as shown in the figure.

	Constant RI		RI Increases(linearly) with height		More RI gradient		RI Decreases(linearly) with height		RI decreases logarithmically

Analytical Solution:

We assume that the ray hits the origin at a given angle of incidence(Θ) and we know the refractive index inside the slab as a function of position. The situation is illustrated in the following figure:

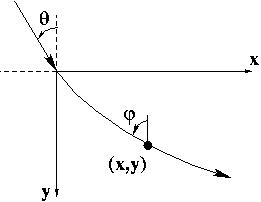
Now we have the following two equations at any point(x,y):

• y'= dy/dx= cot(Φ)
• n(0,0)*sin(Θ)=n(x,y)*sin(Φ) (Snell's law)

We solve the special case when the refractive index varies linearly with height, i.e. n(x,y)=n(0,0)+m*y. Under this condition we can solve the above differential equation and get the closed form solution as:

We also need the length of the curve to find out the time taken to traverse the path(which is used to find the closest intersection in case of multiple objects). For this case the length comes out to be:

Both these formula holds only if there is some linear variation in refractive index(m should not be equal to zero).

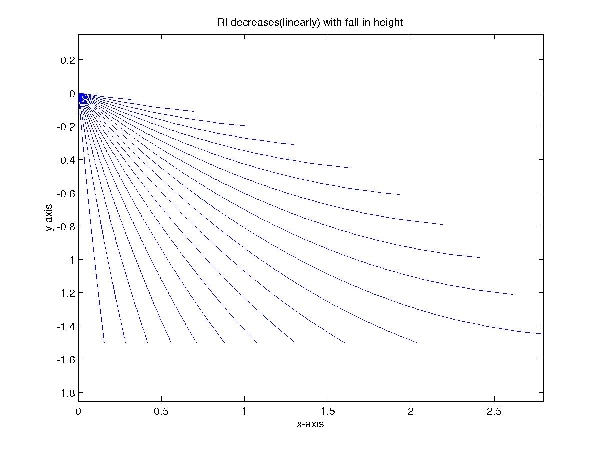
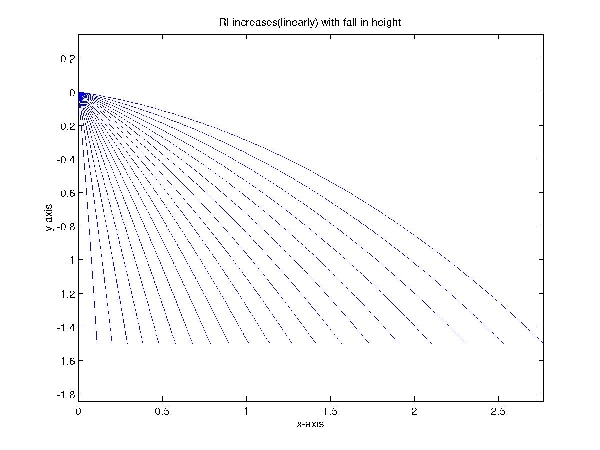
These paths were plotted using matlab under increasing and decreasing the refractive index. We have plotted the path traced by the rays till it reaches a line(y=-1.5) or till we reach a point where internal reflection takes place. The path traced by the rays after suffering internal reflection can be obtained by the same equations after a suitable translation/rotation of the axis.

Below are the images we got using this analytical approach. The left image is a rendering of the scene where the refractive index is constant. The black region in the middle image indicates the area where our analytical method is used to compute the solution. The rest of the image is generated using voxel based ray tracer. The final image(the right image) shows the rendering we got using this hybrid approach. Theses results are more accurate than the piecewise approximation while at the same time is much faster since we do not have to approximate the curved ray path by tiny ray segments.

	Constant RI		Part of the image rendered by voxel-approx.		Rendering using hybrid approach

Here is the source code used for rendering these images.

Conclusion:

References: