Shane Witnov -- Rahul Gupta
(Original Proposal)
TARed Code

Thin-Film Interference
This was implemented by simulating the physics of a real interference pattern on a surface with a single thin layer. The layer was chosen to be 700nm and was then modulated by a noise function. When an eye ray intersected the surface the distance it would travel to hit the inner surface was calculated. This distance was added to the distance the light ray would take to hit the same point. This distance value was compared to the distance that would be required to have perfectly constructive interference for red, green and blue light. Then the RGB values of the incoming light were scaled appropriately and added to the final color of that pixel.

Miscellany TFI Comments
To calculate the background color of the shell, I took the input color for the RIB file, modulated it with a noise function and then added a specular highlight. To get the thin film interference working on more interesting models, I also had to add UV coordinate mapping of nurbs to LRT.

Results
The final renders turned out pretty well. The interference patterns resembled those on abalone shells and seemed to modulate approximate correctly when the view point was changed. Here are some examples of the abalone under different colors of light. In order they are blue/green, blue, green, and red. (Note that the light is not monochromatic, just more strongly in one part of the spectrum). The video shows how the interference changed as the camera moved.

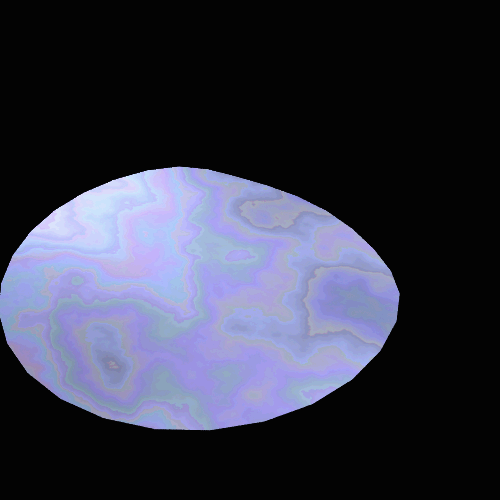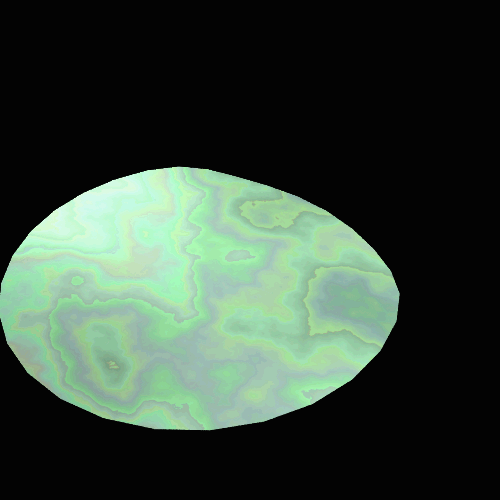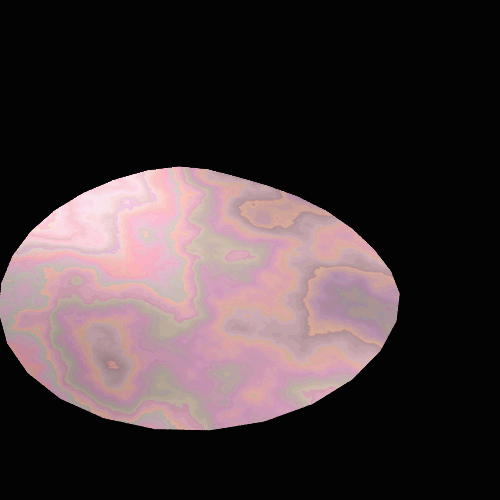
Short Video (Sorenson 3)

Fractal Terrain
As a prelude to bump-mapping the surface of the abalone, we decided to experiment briefly with random terrain generation and texturing in the context of sand-like surfaces, since any abalone image we rendered would look more realistic if placed upon a beach. To that end, we implemented a system based on the "Diamond-Square" fractal algorithm described in:

http://www.javaworld.com/javaworld/jw-08-1998/jw-08-step_p.html

We constructed a new "Fractal" class that generated a randomized grid of Z-coordinates, and then had the heightfield constructor copy this grid, instead of initializing Z-coordinates from a data file. Just for fun, the sand-like color patterns used to texture the heightfield were generated through a Perlin noise function downloaded @

http://astronomy.swin.edu.au/~pbourke/texture/perlin/

The noise function was used as the basis for a random inteprolation between two colors, the result of which was passed to the LambertianReflection() function in Matte::GetBSDF().

Bump Mapping
We decided to bump-map objects by indexing into a heightfield structure using a given facet's UV-coordinate pair. As our test abalone surfaces were 2-dimensional planes, constructing a coordinate system around the original surface normal was straightforward. The normal vector returned from the heightfield was then passed through a facet's coordinate system, with the resulting perturbed normal being used to shade the object. We also experimented with bump-mapping the beach surface. By varying the perturbation amount, we could enhance the bumpiness of the sandy surface without actually recomputing geometry. It would be interesting to further experiment with laying bump maps over heightfield geometry - by animating the U,V coordinates used to index into the bump map, we might be able to "push" shadow-like spots across the surface of the field, and thus simulate simpler versions of caustics and other underwater effects.

Short Video (Sorenson 3)

The above video shows the basic effect of layering a "heighfield as bump-map" over heightfield geometry. By decreasing the perturbation amount over time, one can see the effects of the bump-map fade over time.

Bump-mapped abalone fragments

Short Video (Sorenson 3)