CS 348b Project Proposal

The idea in this project was to render realistic pictures of a Christmas tree covered by snow at dusk. The complex lighting due to the atmosphere and to the small lamps on the tree, the modeling of pine trees and finally the modeling and rendering of snow constitute the main challenges of this project.

1. Modeling Snow

Show is modeled using metaballs. A metaballs is described as an "isosurface," a surface that is defined by checking for a constant value throughout a region in 3D space. In general metaballs can have any kind of basic components but for modeling snow we used only spheres and ellipsoids. Following images demonstrate the process of metaball generations using LRT:

Sphere Ellipsoid
Sphere

Blob with 2 ellisoids Blob with 4 ellipsoids
ellipsoid-blob

    And finally an interesting one:)

The basic implementation of intersections with this primitive use the ideas developed in Persistance of Vision (POVray). We extended it by integrating a kdtree acceleration structure in the blob class for speeding up the intersections when there are many components. This resulted in a speed improvement from 20 min to 3 minutes of rendering time for a blob with 20000 components.

Snow modeling using Metaballs:

To simulate the snow on various objects in the scene we thought of using the ray tracer itself. Snow is considered as a ray coming from some point at infinity with direction determined by gravity and winds. So snow fall is basically a set of parallel rays intersecting the scene. This framework allows to simulate snow coming from any direction and we can put the snow on any kind of object. We can easily control the size/density of snow.

To give a more realistic impression, we are modulating the sphere into a rotated ellipsoid to better model the aggregation of real flakes.

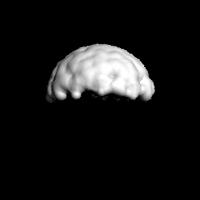
Following example demonstrate the idea where snow is projected on a sphere from above. Figure shows only snow part.

Snow on sphere

Layered Snow Fall: To get the realistic feeling of now we did 2 layer snow projection upper layer having smaller flakes. First layer with big blob element size represent the shape of the object on which ray is projected and second layer present finer details of snow flakes. This reduces number of blob elements required to model snow on a given surface by a large amount. We did not include this in our final scene since we could not get the expected effect, unless we used too many blob components.

2. Modeling Trees:

We really wanted to have realistic looking trees as the base for our image. We created an L-system parser specialized for pine trees, as described by A. Lindenmeyer. It is based on the parsing code written by N. Lambert (Stanford PhD student). We extended his code to account for gravity and to properly model the geometry of a cone-shaped tree. The rules for the main tree are the following:

Axiom: \(100)O(0)D
O(t) : (t<=3) ==> ASASASASO(t+1)
S ==> L(0.9)!(0.85)+(0.5)
A ==> E[&L(0.85)!(0.45)B]\(81)[Z&L(0.8)!(0.4)B]\(75)[&L(0.85)!(0.45)B]\(74)[Z&L(0.8)!(0.5)B]\(78)[&L(0.75)!(0.4)B]\(75)
B ==> YF[-L(0.8)!(0.9)WC]L!(0.9)C
C ==> YF[+L(0.8)!(0.9)WB]L!(0.9)B

The main difficulties that we encountered in the modeling were to find this formula and to make the needles look nice. The rules we use are very simple: O accounts for the trunk, S for the transformations that occur along the trunk, A for the main branch structures, B&C, that recursively call each other for the small branches. The non standard symbols Y and W account for gravity.

The needles are modeled by elongated ellipsoids. They are pointing with a relative direction of 30 degrees with respect to the branches (omitting the gravity effect), and disposed randomly along the branches. Their size vary as a function of their position in the tree.

After we made our first tree, it was easy to create a new model for each of the trees in the picture, by tweaking the parameters slightly.

3. Glowing lights:

How can we integrate so many lights in the scene without taking too much computation time ? We have approximately 150 lights in the main tree and one in the moon. Using area lights would have been suicidal, so we opted for point lights with a nice camera-glowing effect.

The glow is an approximation of both the atmospheric effect and the spread of the light on the camera film. The idea is to take the intersection of a ray from the camera with the plane of the light source and to compute the distance between this intersection and the light source. We use an exponential falloff formula on the intensity of the light.

The main issue here was to get the right parameters, so that the glow was not too weak or too strong, allowing for all the other lights in the scene. We also spent some time optimizing it since the distance computation has to be made for every point in the scene multiplied by every glowing light.

4. Global illumination:

Finally, to get the soft feeling of lighting from the scattering atmosphere, we implemented photon mapping. The problem here was computation time. We put a lot of effort into optimizing this part.

First, we implemented H. Christensen's technique of irradiance precomputation. It speeds up the final gathering step by a factor of ten.

Then we limited the sampling of photons to the snow surfaces, as needles and branches would not account for much of the diffuse lighting anyways. In order to get photons from the sky, we treat it as a light source infinitely far from the scene that emits low intensity light from every position on the hemisphere. Final gathering rays that go to infinity are given the color of the sky. That is how we get the blue coloration of the whole scene.

5. Subsurface Scattering of snow:

Subsurface scattering to model the translucency of snow is motivated from the Jenson's paper "A Rapid Hierarchical Rendering Technique for Translucent Materials". Implementing this method for snow gives couple of interesting challenges:

Sampling the metaballs: Uniform sampling the area of metaballs is itself a challenging problem. We devised a simple sampling algorithm that works as follows:
For each sphere (or ellipsoid) in the blob we generate rays originating from the sphere center and having uniformly distributed direction in the sphere. The intersection points of these rays with the blob that lies within the sphere are calculated. Then these points are checked against the sample points on blob from the neighboring spheres. Those sample points which are at a distance less then some threshold from any of the neighboring sample points are rejected. Following picture show the sampling points for "snow on sphere picture" (top view)

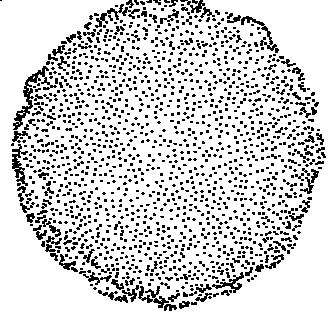
Another issue with sampling was "how to make sure that it is uniform and all the samples points have distance less than lu as needed for the implementation of subsurface scattering". We did testing using finding mean min-distance and variation to quantize the non-uniformity of sampling.

Following example shows one example which we generated from our implementation of Jensen's paper. There are two light sources in the scene. First light source is on the side and other is a red light in the back side of scene.

A blob without Translucency	With Translucency

    Snow without translucency



   Snow with translucency



    Snow without subsurface scattering

    matte


    Snow with subsurface scattering

    another

6. Miscellaneous:

There are many other details in the picture that we worked on. We are just mentioning a few here...

Textures
First, we have icy water texture on the foreground based on a very hacked version of the windy displacement mapping in LRT. It is projected on a simple polygon, and gives the right impression of half-frozen liquid element. We also have cylindrical mapping of a procedurally generated texture on the trees and a procedurally generated background for the sky (applied as a texture).

Acceleration
We used the KdTree acceleration structure from LRT but we had to modify it to make it work on the scene. The main issue is that we have very large objects (quasi infinite plane, moon), and at the same time very small details (needles). That is why we create one Kd-Tree per group of shapes that belong to the same object. We end up with 20 of these Kd-Trees, that we put into a top level Kd-Tree.