
CS348B - Image Synthesis
John Pau
Date submitted: 8 June 2005
Original project proposal can be found here.
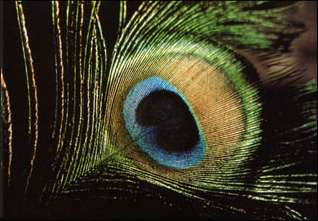
The iridescent colors of peacock tail feathers are primarily the result of structural properties within the feather--not from multi-colored pigments (although pigments are present). Varying densities of melanin granules layered within keratin give rise to thin film interference, which causes iridescence.
In reality, the melanin granules and keratin layers form a regular lattice structure that scatters, absorbs, and reflects incoming light. To reduce complexity, however, the "eye" of the peacock feather was modeled as a single layer of thin film. As a consequence of this phenomenological approach, the computed reflectance will be higher than the actual reflectance because internal scattering and absorption are ignored. Using the single layer model, the two key parameters are: the index of refraction of the layer and the film thickness. The paper by Jian Zi et. al. describes the thickness of each keratin layer in the blue barbules as 140 nm and the index of refraction of keratin as 1.54.
A single peacock feather was modeled within 3D Studio Max 4. Due to the high density of barbs near the "eye" of the tail feather, I made an early decision to model that area with a single flat disk. This approach turned out to be too simplistic, as can be seen by the incongruity at the seams of the disk and the surrounding barbs. Even using an alpha mask to hide the circular shape of the disk does not help to make the "eye" blend into the rest of the scene. As an alternative to the disk approach, I would consider modeling every single strand of the feather and use multiple 1D texture maps to control the change of colors along the barbs.
The barbs were created using the loft feature within the software package. For each barb, a line was drawn to control its length and curvature, and a circle was traced down this line path to create a tube shaped object. After the loft, the barb was converted to an "editable mesh", which allows selection of individual vertices and faces for fine-tuning of barb placement and appearance. For example, the endpoints of certain barbs were rotated to conform to the rachis, or the main "stem", of the feather. Also, the tips of certain barbs were squeezed together to give a tapered appearance.
After constructing the feather geometry, I exported the scene as a .3DS file and used the 3ds2lrt tool to create an .lrt file. I modified 3ds2lrt to automatically assign the desired material properties to each portion of the feather: the rachis, the "eye", and the barbs. Fortunately, pbrt rendered the .lrt extension file without issue.
The key feature required to implement interference colors is a spectral representation of light. Following the short note by Glassner and the pre-computed phosphor matrix given in pbrt's Spectrum class, I used the three given fitting functions to compute the matrix D. Multiplying the inverse of D with RGB values yields 3 weights for the fitting functions. The weighted sum of these fitting functions is the value for the spectrum at specific wavelengths. A total of 95 wavelengths were used to represent the spectrum, which is the approach taken by Steve Bennett and Arthur Amezcua in their CS348B project from Spring 2001.
After the spectrum for the incident light was found, I computed the phase difference at each wavelength of the light using the viewing angle, a 1.54 index of refraction, and a thin film thickness of 140 nm. The equation for phase difference is found in Gonzato and Pont's paper and is given as: phase_diff(lambda, theta) = (4*PI*d/lambda)*sqrt(nf*nf-na*na*sin(theta)*sin(theta)) + PI, where d is the film thickness, nf is the index of refraction of the thin film, na is the index of refraction of air, and the final PI term accounts for the phase change of incident light reflected at the air-film interface. Reflection from a low index to high index of refraction results in a 180 degree phase change. Using the phase difference, Gonzato and Pont compute the reflectance as cos(phase_diff(lambda,theta))*cos(phase_diff(lambda,theta)).
Three texture maps were used for the peaoock feather: a color texture, a bump map, and an alpha mask. The color texture defines the characteristic "eye" pattern seen on peacock tail feathers. Iridescence computations were only performed for points that were mapped to blue. A bump map was required to create the subtle ridges and grooves of the peacock feather. Finally, an alpha mask was added with the intention of making the borders of the circular disk conform to the layout of the surrounding barbs.
 |
 |

The blue barbules are rendered using iridescent color. The subtle difference in color between the upper and lower portions of the blue patch are due to the change in viewing angle. |
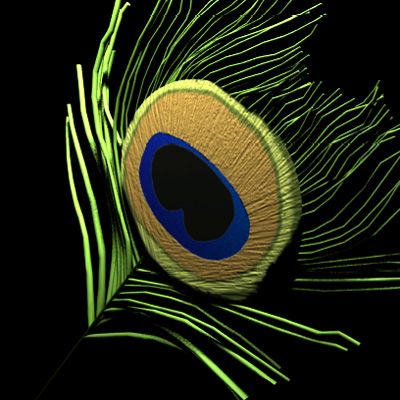
As the viewing angle becomes more oblique, the interference color shifts to lower wavelengths. At greater angles, the "eye" of a peacock feather can take on a deep purple hue. |
References