Geometrically Stable Sampling for the ICP Algorithm
|
Natasha Gelfand Stanford University |
Leslie Ikemoto Stanford University |
Szymon Rusinkiewicz Princeton University |
Marc Levoy Stanford University |
Fourth International Conference on
3D Digital Imaging and Modeling
(3DIM 2003)
October 6-10, 2003
|
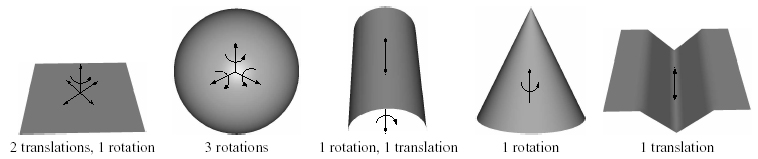
| By analyzing the eigenvalues and eigenvectors of the covariance matrix derived from the points on the shapes, we can determine that the above shapes are unstable. Below each figure is the number and type of instabilities. The axis of unstable rotation and direction of unstable translation are indicated on the shapes. |

|
| Points picked by our algorithm to constrain the unstable motions of a patch with two grooves. (a) Points constraining two unstable translational eigenvectors. (b) Points constraining unstable rotation. (c)-(d) Two remaining rotations are stable so they only require a few points. The eigenvector corresponding to translation in z is well constrained by the already picked points and does not contribute to the sampling. |