Assignment 6 - Image Matting and Composition
Due Date: Thursday March 1st, 11:59PM
Questions? Check out the Assignment 6 FAQ and discussion page.
In this assignment you will write code to separate a foreground object from a constant color background in an image and then place this foreground object in another scene of your choosing. In computer graphics terminology, you will extract (or lift) a matte from an image to isolate a foreground object, and then composite the foreground object with a new background using the matte. With such technology you can whisk your beloved TAs off to far away lands and exotic beaches where they no longer have to grade homework assignments.




Download and build the starter code
1. Begin by downloading the Assignment 6 starter code and latest version of the libST source here. Libst has not changed in this assignment, but we are bundling it in with the assignment zip file just like in all the previous assignments.
2. Build the code. In this project, you will be modifying assignment6/matting.cpp. In the assignment6/ subdirectory we have placed a couple of image files. The files doodle.png, elephant.jpg, and kayvon.jpg are sample images of objects placed in front of a green screen. This directory also contains a number of backgrounds to test compositing the extracted foreground objects into. In this assignment you will also be given the opportunity to take your own pictures against a green screen.
Review of Premultiplied alpha
Recall from class the definition of pre-multiplied alpha. If a surface or image pixel has color C=(r,g,b) and opacity = a, we can either store the information as (r,g,b,a) or as (ra,ga,ba,a). In the later case, alpha has been premultiplied in with the component values for the color. This is useful for both performance and convenience, and is the representation I will use throughout this assignment. For example, the premultiplied representation of a 50% transparent white surface is (.5,.5,.5,.5). In this assignment, when I refer to the color C, you should assume its components have been multiplied by alpha.
The Problem
Given an image of an object in front of a green screen, we want you to estimate the color and transparency of the foreground object for each pixel of the image. Unfortunately, given only a single image of the foreground object, it is impossible to analytically determine both the color and transparency of the foreground object even if the background color is known. For example, a brown pixel in the image might be the result of an opaque brown foreground surface, or it may be the result of a semi-transparent red surface in front of the green screen. The following is a summary of the mathematics of the problem.
To begin, recall the compositing equation from lecture: The color produced by overlaying a foreground color with opacity=alpha over a background color is:
C = Cf + (1-alpha)*Ck * 'C' is the color of the observed image pixel. * 'Cf' is the color of the foreground object with pre-multiplied alpha. * 'Ck' is the color of the background object * 'alpha' is the opacity of the foreground object (alpha=1 for an opaque object)
I will refer to Rf, Gf, and Bf as the red, green, and blue components of the foreground color (The same goes for R, G, B, and Rk, Gk, Bk respectively). Recall, these values contain premultiplied alpha. Since we are filming in front of a green screen, we assume we know the value of the background color Ck. Therefore, the equation above represents a system of 3 equations (corresponding to each color channel) with 4 unknowns:
R = Rf + (1-alpha)*Rk G = Gf + (1-alpha)*Gk B = Bf + (1-alpha)*Bk Rf, Gf, Bf, and alpha are the unknowns.
Clearly, the system is under constrained, so there an infinity of solutions to this problem in the general case, and as is often the case in graphics the particular solution we want is the solution the "looks right". As discussed in lecture one way to constrain the space of solution is to assume that all foreground colors have the magnitude of their blue component related to the magnitude of the green by some ratio k2 (that is: Gf=k2 * Bf). This assumption is equivalent to saying that all foreground colors lie in a plane in color space. It is called the Vlahos assumption, and is named after Petro Vlahos who used this technique to perform matte extraction on traditional film in his company's Ultimatte machines.
By the equations above, the observed image color C is a linear combination of the background color and a foreground color lying on this plane. The weighting of the combination is given by the opacity alpha of the foreground surface. We illustrate this with the following diagram in the GB plane of color space.
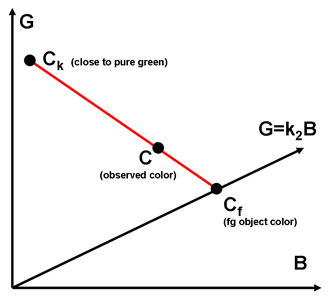
The following is a derivation of how alpha can be determined using the Vlahos assumption.
Let A be a vector representing the plane foreground colors lie on. A = [0 1 -k2 0] Then for all colors Cf = [Rf Gf Bf af] on the plane, Cf dot A = 0, and observed image color C = [R G B a] and background color Ck = [Rk Gk Bk ak]
C = Cf + (1-alpha)*Ck Cf = C - (1-alpha)*Ck 0 = Cf dot A = C dot A - (1-alpha)*(Ck dot A) C dot A = (1-alpha)*(Ck dot A) alpha = 1 - (C dot A) / (Ck dot A) By the definition of the plane A: C dot A = G - k2*B So... alpha = 1 - k1 * (G - k2*B) where k1 = 1 / (Ck dot A) is a constant since it is assumed we know the background color Ck
The code
The matting application accepts two arguments: The name of the source image and the name of the new background image to composite over. For example, a good initial test is:
./matting doodle.jpg newyork.jpg
There are a number of useful UI features you should know about in this assignment.
- The '+/-' keys toggle the display of various images including: the source image (the original image in front of the green screen), the composited image (containing the extracted foreground on a new background), a greyscale visualization of the foreground matte (white=opaque), and the new background image by itself.
- Pressing 's' will save the current image on screen to disk.
- Clicking the mouse will print out the color of the source image pixel under the cursor as well as the value of the matte at this position.
- The arrow keys can be used to modify the values of k1 and k2 used in the Vlahos algorithm.
- Pressing 'c' will set the estimate of the background color to be the value of the source image pixel under the mouse cursor, and trigger the matte to be extracted.
Step 1: Matte extraction
You will need to implement the routine extract_foreground in matting.cpp. This routine accepts as input a foreground image 'src' and should compute both the opacity and color of the foreground for each pixel. It also accepts k1, k2, and an estimate of the background green screen color as arguments. For each pixel in the source image: You should do the following:
1. Estimate alpha. We leave this up to you in the assignment. A first pass implementation should use the formula for alpha derived above
alpha = 1 - k1 * (G - k2*B)
You will need to modify the constants k1 and k2 to produce a good matte for your image. This can be done dynamically in the app using the arrow keys. THINK ABOUT WHAT K1 and K2 SHOULD BE by understanding the proof above. There is an intuitive notion for what both parameters mean.
2. Once alpha is known, you can solve for Cf using the compositing equation. Remember that alpha should be premultiplied into the color components of Cf as well as written into the pixel's alpha channel.
Rf = R - (1-alpha)*Rk Gf = G - (1-alpha)*Gk Bf = B - (1-alpha)*Bk
3. For debugging, we'd like you to write alpha into the color components of the image matte. This allows the alpha matte to be visualized when toggling through the applications various display modes.
Visualizing your matte directly is a simple way to test your matte extraction code helpful before you have implemented compositing.
Step 2: Implement Compositing
You now will need to implement the method computeComposite, which takes the foreground color image fg as well as a background image bg and should composite the {{fg}} over {{bg}} and place the result in the image composite. This is a simple application of the compositing equation for each pixel.
Step 3: Make Sure Your Code Works for doodle.png
The source image doogle.png was carefully constructed in Photoshop so that all foreground objects (the circles and brush strokes) have the same ratio of green and blue. Thus, the matte extraction algorithm described above will extract a near perfect matte with correct choices for k1 and k2. It you look at the image carefully, the edges of the foreground shapes are blended (anti-aliased) with the background and thus have transparency. In addition, several of the foreground circles are partially transparent. The examples below show a correct matte extraction from the source image.



A zoomed view of the matte illustrates the transparency in the foreground.

Step 4: Improving Matte Extraction
Vlahos' technique begins to break down when the foreground object contains colors that diverge from the Gf = k2*Bf plane. If you attempt to apply this algorithm directly on real world images (such as elephant.jpg and kayvon.jpg), you will find it difficult to obtain a good matte. We would like you to attempt to improve on the algorithm so that your code can extract mattes from a wider variety of images, such as those you take yourself in the next step. Here are some suggestions and ideas to think about.
- In real world images, despite great care in a green screen setup, the background color is never exactly constant through the image (due uneven lighting on the green screen, shadows cast by actors, noise in the camera).
Vlahos' patent states that better results can be obtained by using min(bgcolor.g, G) instead of just G in the formula for alpha.
The algorithm described above estimates alpha by changes in the ratio of G and B. How could you use the R channel as additional information to improve the estimate. I have found that the following formula yields interesting results. Notice that when k3=1 the formula is the same as the original Vlahos formula.
alpha = 1 - k1 * ( min(bgcolor.g, G) - k2 * (k3*B + (1-k3)*R) )
- Perhaps using a different values for the parameters at different points in the image yields better results. There is no correct answer here, matte extraction is a difficult problem. We would love to see you design an algorithm that can extract a matte (with any user provided help you'd like to add to the interface) as best as possible.
Step 5: Parameter Shortcuts
Before final handin, please follow the instructions in the code so that pressing the F1, F2, F3, etc keys has the functionality of setting parameters up so that matte extraction is the best you can do for the 3 sample source images. This will require modification of the function specialKeys.
Step 6: Take your own pictures in front of a green screen!
Lastly, you will need to come by to take pictures of yourself (or objects of your choosing) in front of a makeshift green screen in the graphics lab.
Please come by Kayvon's office, Gates 381, during one of the following times:
- Tuesday 11am - 12:30PM
- Wednesday 3:00PM - 4:30PM
Do you best to make one of these time intervals, but let me know if special arrangements are necessary.
Additional hints and tips
- Make both the source and new background image you use are the same size.
Notice that the "green" backgrounds in the images we provided are not pure green (0,1,0). This implies that the choice of values for k1 and k2 are slightly coupled. You might want to automatically compute one in terms of the other once a background color is chosen.
Be careful about clamping and overflow. We recommend performing all math on floating point values (you can use the STColor struct), clamping these values to the 0 to 1 range, and then converting back to integers in the range 0 to 255 for storage as pixels.
- TA experimentation has shown that darker pixels (lower luminance) tend to have a higher ratio of green to blue than well illuminated pixels.
Submission Instructions
We would like the following items to be placed in a zip file called LastnameFirstnameAssgn6.zip as handin for this assignment.
Your modified copy of matting.cpp
- Please be sure that you have implemented the event handlers for the F1, F2, F3, and F4 keys. Pressing these keys should set parameter values for that the best matte is extracted for the various sample images (See comments in the code).
- Your favorite picture you took in front of the green screen (and any background image to go with it).
- Answers to the following questions:
Attempt to describe the "meaning" (physical significance) of the parameters k1 and k2 in the original Vlahos algorithm.
How did you find the correct parameter values to extract a matte for doodle.png?
The Vlahos algorithm assumes a certain ratio of blue and green for all foreground objects. How is the estimation of alpha wrong when the object has significantly more blue than expected?
- Please describe any improvements you made to the Vlahos algorithm and tell us how they worked out. Feel free to include a few extra examples of images (or create a web page) if you got creative in inventing new techniques. Which sample images could you not extract a satisfactory matte for, and why do you think this is the case?
Please email this zip file to cs148-win0607-staff@lists.stanford.edu before the deadline. Please make the subject line of this email "CS148 Assignment 6 Handin".
Grading
- 1 point: significant errors in base algorithm implementation
2 points: errors in matte extraction from doodle.png. Algorithm implemented but parameters likely wrong.
3 points: perfect matte extraction from doodle.png + answered questions correctly + submitted own composite photo
4 points: perfect matte extraction from doodle.png + answered questions correctly + submitted own composite photo + brief exploration of improvements to base technique so that code can extract mattes (but not necessarily flawless ones) from all sample images. Implementing the modified 3-parameter version of Vlahos described above is enough to get full credit on the coding portion of this assignment.
We are willing to give up to 1 point of extra credit for amazing work improving on the matte extraction algorithm.