Assignment 8 - Subdivision Surfaces
Due Date: Thursday March 15th, 11:59PM
Questions? Check out the Assignment 8 FAQ and discussion page.
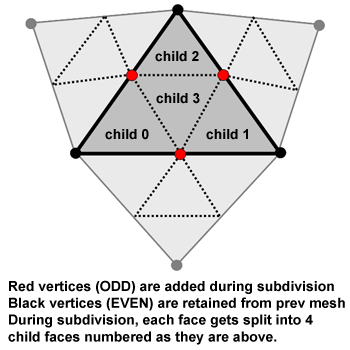
In this assignment you will implement subdivision of a triangle mesh using a technique referred to as loop subdivision. Conceptually, this is very simple. In each stage of subdivision, every triangle of in the mesh is split into 4 triangles and every edge in the mesh is split into two edge connected by a new vertex. The difficulty in this assignment arises from the need to efficiently manipulate a mesh data structure to perform successive subdivision operations.
Download and build the starter code
1. Begin by downloading the Assignment 8 starter code and latest version of the libST source here. Libst has changed in this assignment. We've added a new class STVector, that should assist you with operations on 3-vectors. You will be performing many such operations in this assignment.
2. Build the code. In this project, you will be modifying assignment8/subdiv.cpp. In the assignment8/ subdirectory we have placed two sample meshes tetra.shp (a tetrahedron) and sphere.shp (a sphere) for you to test your code on. Run the program using the command subdiv mymeshfilename.shp and you will see an image of the mesh rendered in wire frame on your screen. Notice that we've added some mouse controls that move the camera in this assignment, making it easier to view a 3D object. Dragging while holding the left mouse button rotates the camera around the object. Dragging with the right mouse button depressed zooms, and dragging with the center button depressed will dolly (translate) the camera.
Mesh Representation
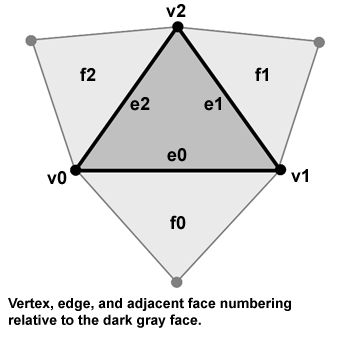
The most important part of this assignment is understanding how the mesh is represented. We will be working with triangle meshes in this assignment, so each face contains exactly three vertices: They are labeled v0, v1, and v2 in the diagram below. In this assignment we will only be working with "closed" meshes, so each face is connected to another face on each of its three edges. The adjacent faces are labeled f0, f1, and f2. Lastly, we've labeled the edge between vertex i and (i+1) mod 3 edge i.