Revision 10 as of 2007-06-11 09:41:54

Final Project

Group Members

Andrew Yen
Laurie Kim

Intro

For our project, we intended to render a realistic image of soap, accurately capturing its subsurface scattering properties and surface geometry.

Techniques Implemented

Subsurface Scattering

In order to model the subsurface scattering of light through soap, we followed the implementation outlined in "A Rapid Hierarchical Rendering Technique for Translucent Materials" by Jensen et al. The basic approach was to do a two-pass rendering process. The first pass was to calculate irradiance samples on locations over the subsurface scattering object. On the final rendering pass, the irradiance sample values are used to calculate a dipole approximation of light scattering through the translucent material.

We added a Subsurface class to pbrt to represent a subsurface scattering object. The Subsurface class stored references to all the primitives that made up the object, as well as maintained an octree to efficiently store irradiance samples over the object. The octree was used to quickly approximate far away samples when the solid angle subtended by the samples was less than a specified threshold. We took uniform samples using stratified sampling over the primitives that made up each object. The number of samples was first determined by the area of the primitive divided by a disk with diameter of the mean free path. We then increased the number of samples as necessary in the final images to eliminate artifacts.

In calculating the exitant radiance at a point on the subsurface scattering object, the Subsurface class omitted the single scattering term since for highly scattering objects with albedo close to 1, the multiple scattering term dominates. We also assumed a diffuse radiance at the surface as light exits the material. We modified the SurfaceIntegrator interface to allow various surface integrator classes to implement how to calculate the irradiance at points on a surface. The irradiance samples were calculated during the preprocessing step prior to rendering. In particular, we modified the DirectLighting integrator to uniformly sample all lights to approximate the irradiance at a point. We also modified the PhotonMap integrator to calculate irradiance by taking into account the global illumination in the scene.

During the rendering pass, each integrator needed to be modified to react differently when encountering a subsurface scattering primitive. The diffuse term came from the dipole approximation described above, but the glossy and specular terms in the BRDF functioned as before.

Models and Geometry

We modeled our soaps after the Marseille style Bonne Mere soaps from L'Occitane:

We originally modeled our soap as a relatively simple block using Maya. We intended to use bump mapping to show the surface details. However, we found that using bump maps didn't generate as dramatic and interesting surface details as we had hoped for. Subsurface scattering tends to smooth out small bumps on the surface, thus making bump mapping a less effective technique.

We decided to use displacement mapping instead to model the writing and decorations on the soap. We used scanned images of the soap surfaces as displacement maps to perturb the subdivided mesh in Maya.

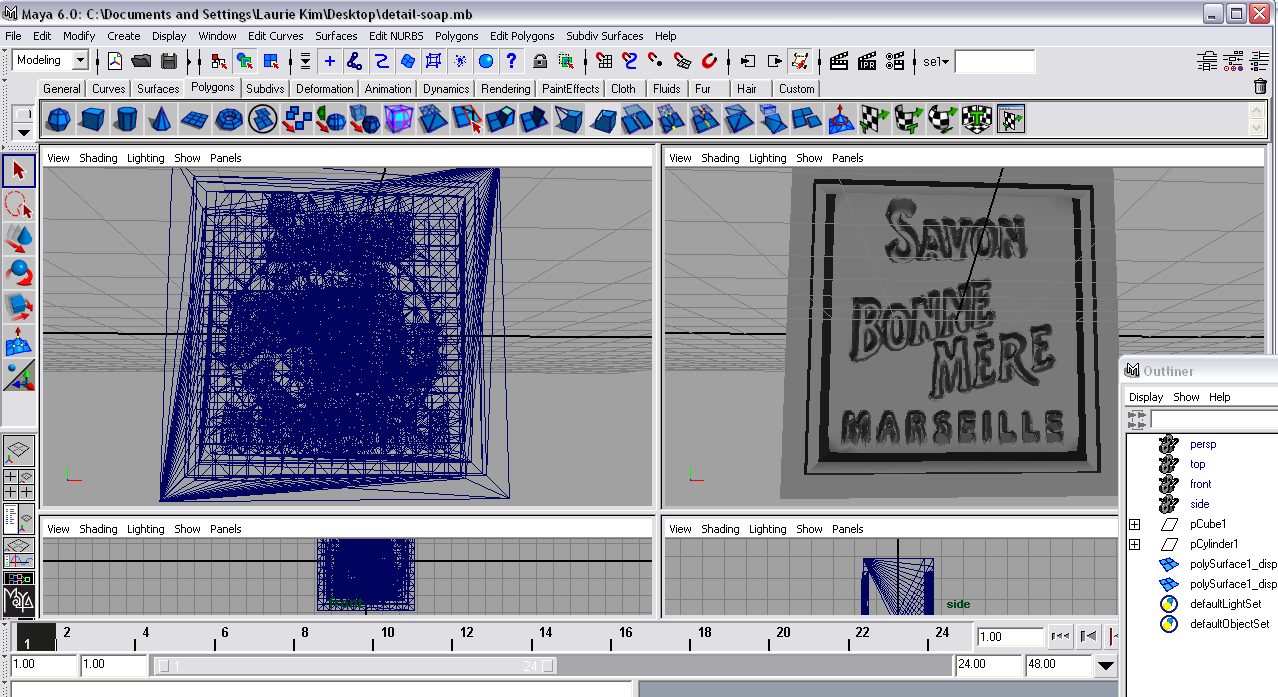
Modeling surface features as actual geometry also helped produce more accurate scattering effects around the details.

Color Matching

Another part of the challenge of reproducing the look of our soap was in figuring out the scattering parameters to match the soap colors. The parameters that are necessary for the dipole approximation are the reduced scattering coefficient and the absorption coefficient. We started out with a target diffuse material color and a target dominant scattering color that we wanted to aim for. We then used the equation in Jensen et. al's "A Practical Model for Subsurface Light Transport" which related the diffuse reflection coefficient to the reduced albedo of a material to solve for the reduced albedo. Since this equation is not easily invertible, we plotted 100,000 points along the Rd vs. albedo curve and linearly interpolated the albedo value from the target material Rd value for the RGB channels. We then used the ratios of the scattering color to modulate the maximum diffuse mean free path of some known material such as those listed in [2]. These new mean free path values were then used to calculate the scattering coefficients.

These are example results rendered using our calculated parameters for the same material and scattering colors but different mean free path values modeled after measured materials:

These are the final parameters we settled on for several soap colors:

Technical Challenges

Results/Conclusions

Work Breakdown

References

Pat Hanrahan and Wolfgang Kreuger: "Reflection from Layered Surfaces due to Subsurface Scattering". Computer Graphics (Proceedings of SIGGRAPH 1993), July 1993.

Henrik Wann Jensen, Stephen R. Marschner, Marc Levoy and Pat Hanrahan: "A Practical Model for Subsurface Light Transport". Proceedings of SIGGRAPH 2001.

Realistic Image Synthesis Using Photon Mapping by Henrik Wann Jensen