Physically Realistic Volume Rendering
Group Members
James Hegarty
Qiqi Wang
Overview
In this project we are planning on rendering a scene based on a physically accurate light scattering model for volumetric materials. Such materials can include fire, smoke, vapor, and clouds. Special effects such as rainbows can be also rendered with this model. In order to accurately model the distribution of volume materials in complex geometry, a physically based fluid calculation must be performed, resulting in an unstructured mesh. A ray tracing algorithm for unstructured meshes needs to be developed, and light reflection and scattering models from these volume materials needs to be built.
The following pictures are from www.ImageMontage.com , I believe they are taken at the Nevada fall in Yosemite. The waterfall and rainbow is the type of things we want to render.
|
|
|
Modeling of volume material distribution
In order to model the distribution of volume materials accurately, we will use the commercial flow solver Fluent. In the waterfall scene, we use commercial Commputational Fluid Dynamics software Fluent 6.2 to calculate the flow of air around the waterfall, as well as the density of water drops in the air. The size of the mesh is 1000 ft by 1000 ft by 6000 ft, the waterfall alone is 100 ft tall. The following pictures demonstrates the mesh generated for the Computataional Fluid Dynamics calculation. The first picture shows the surface mesh, the second picture shows the volume mesh on the symmetric section plane.


This is a typical unstructured mesh used for Computational Fluid Dynamics calculation around complex geometry. First of all, tt has huge mesh size variation. The cells inside and near the waterfall is small, and the cells away from it is ten thousand times larger in volume. Also, it has three different types of cells. Inside the waterfall, octohedral cells are used; away from the waterfall, hexahedral cells are used; pyramid cells are used as a layer between octohedral cells and hexahedral cells.
The velocity field and the density of water drops are computed by Fluent 6.2, a most up-to-date commercial Computational Fluid Dynamics software. The small volume in the middle of the step is used to model the water fall, and the rest of the volume is used to model the air. The flow field is calculated using incompressible Navier-Stokes equation with k-e turbulence model. We model the driving force by the flow of water inside the waterfall as a constant downward source term in the momentum equation. This source term drives the flow field in the entire volume. We model the floating water drops in air as transporting and reacting chemical species, whose density is also solved by Fluent 6.2. Inside the waterfall volume, the water drop density is generated in a constant rate. In the rest of the volume, the water drops evaporates into vapor and convects away from the waterfall. The following two images shows the flow field on the symmetric cut plane and the isosurface of 20% of the maximum water drops concentration. Our rainbow image is rendered based on this calculated density field of the water drops.
Ray tracing through unstructured mesh
There is some work done on ray tracing algorithms for volume effects, but most of it is restricted to cartesian meshes, which limits its ability to model flow effects in complex geometry. We will base our volume rendering on a ray tracing algorithm for unstructured meshs such as the mesh shown above. We expect ray tracing of unstructured meshs to be much more expensive than ray tracing of a cartesian mesh, but it is potentially very rewarding. It allows us to render volume effects that is directly produced by the flow solvers.
Modeling of light scattering
|
|
|
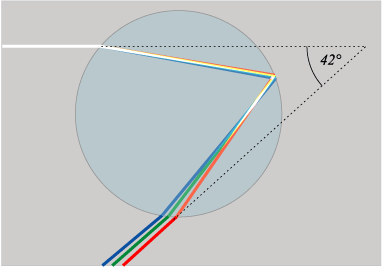
We will use a physically-based model to simulate the scattering of light in volumes. Our model will cover scattering with opaque particles such as smoke, in addition to transparent particles such as water. In the case of transparent particles, light of different wavelengths has different refraction indices inside the particle, and internal reflection occurs, leading light that enters the water droplet from behind the observer to reflect back at the observer spread out horizontally. This effect is commonly known as a rainbow. Our model will not involve ray tracing of individual particles, because this would require a prohibitive amount of calculation time. Instead, we will make simplifying assumptions based on the light and camera angle and properties of the particle being rendered.
While PBRT does already include some models for volume rendering, they do not account for transparent particles and angle dependent effects, like we want to render. We also suspect that there may be the possibility of improving PBRT's efficiency in rendering our volumetric meshes.
Sources
Rainbows, Halos, and Glories by Robert Greenler