An Introduction to General Game Learning

Presentation version: PDF, PowerPoint

General game learning (GGL) is the idea of developing an algorithm that can learn how to play arbitrary games by interacting with them. The computer is only provided access to a video feed of the game and is allowed to issue commands such as moving the mouse or pressing buttons on a controller. This is very different from traditional game AIs which already know all the rules of the game and are tightly optimized to make intelligent decisions in the specific game they are written to play. Attempting to generalize these systems is the goal of GGL, which is a rich topic and the task of developing an effective game learner will require combining a diverse number of challenging computer science problems. To make the task more tractable, we will sometimes use a semi-supervised learning approach where the AI also takes as input segments of humans playing the game. The AI can use these to determine what kind of actions are likely to affect the game state, what the goal of the game is, or what strategies might be effective in achieving the goal.

We start by sketching the pipeline stages of a game learning system. A good general game learner starts by breaking down each frame of the game into meaningful components such as "the black king" or "a goomba": we call this a symbolic representation of the game. It then needs to learn rules that govern these entities such as "black kings can move to adjacent squares so long as these squares are either empty or contain white pieces and doing so does not cause the black king to be threatened by a white piece" or "goombas move either left or right on horizontal surfaces at a rate of 3 pixels per frame, unless they are not supported by a horizontal surface in which case they move downward at a rate of 7 pixels per frame". Using these rules it can determine how the symbolic representation changes with respect to time or player actions. A learner also needs to guess the goal of the game, such as "capture the black king" or "reach Princess Peach at the end of world 9". Using this knowledge, it can develop a strategy for reaching the goal such as "capture black pieces without losing white pieces" or "move to the right without dying". Finally, a general game learner needs to combine all of this knowledge together to execute intelligent actions that achieve the goal, and continuously update its internal beliefs as it is presented with new observations and evidence.

General game learning is not yet a well-developed field. This document serves to introduce a reader to the topic and describe how it fits into existing fields so is consequently fairly long. If you are mostly interested in the technical aspects of implementing a general game learner you can skip to the pipeline section.

Motivation

At first glance research in general game learning might seem like a fun project but not necessarily a very useful or important topic. After all, even if it were reasonably effective at learning new games, a general game learner would likely be inferior to existing special-cased AIs such as those found in Chess programs or enemy players in StarCraft. Since the purpose of most games is for humans to derive enjoyment from playing them, it just doesn't seem like there are many applications for a computer to learn to play an arbitrary game except in those cases where a dedicated opponent is needed. Such a viewpoint comes about because the term "digital game" often conjures a very narrow range of applications such as Mario or Solitaire and does not seem to apply to the "real world". It is easy to forget that, to a computer, all information must ultimately be filtered through a digital lens: from a computer's perspective there is no difference between the task of controlling a Roomba, and playing a game where the objective is to vacuum the floor of a house given readings from a certain set of input sensors. Almost any interesting and useful task can be cast as a digital game -- whether or not the controls are for a robot or an accurate digital simulation of the environment is irrelevant from the perspective of learning. Such tasks might include driving a car, paying your bills, or folding your laundry. Digital games are a starting point for learning such general tasks because they offer a well contained environment to operate in with a goal that can be easily, objectively, and quantitatively evaluated. Once we are able to produce effective general game learners for digital environments, we can start to look at their effectiveness on games where the inputs are sensors in the real world.

Human Learning

We can gain insight into ways to learn general games by looking at what methods humans use to learn games. There is no single pathway through which humans learn something: we aggregate knowledge from a variety of sources, and continue to iteratively update our knowledge of the subject as we are presented with new observations or sometimes just by thinking about the subject in question. The case of learning games is no exception. Here we show a few of the components of the human learning process when we encounter a game that we don't know how to play:

This list is by no means exhaustive. When developing a general game learner, we would like it to learn from as many sources as possible. With no exceptions, attempting to tap each of these sources of knowledge requires effective solutions to extremely challenging problems in artificial intelligence. Let's look at some specifics:

Learn rules by reading them — One way to learn a game is to read the associated rulebook or Wikipedia page. Attempting to have a computer learn useful knowledge from a rulebook touches upon several interesting natural language problems such as textual entailment, relationship extraction, and co-reference. Furthermore, most useful rulebooks are not just text but also contain important visualizations that must be parsed to fully understand the rules, such as the figures for the moves of a queen and knight shown above. Although natural language processing and visualization understanding are not currently accurate enough for these information sources to be useful to a computer for the purpose of general game learning, in the future it might be possible to use them to augment an existing learning system.
Learning by recognition and experience — With almost no exceptions humans never encounter a situation in which they have absolutely no prior experience or expectations. When playing Mario for the first time, when we move Mario off the ledge of a platform we are not surprised to see that he falls, because Mario is a solid object and, in our experience, most solid objects are affected by gravity and fall when they are not supported from below. Likewise when we first encounter a Koopa Paratroopa we are not surprised that it is not affected by gravity because we recognize that it has wings and in our experience things with wings can fly. For almost every object we encounter in a game we have some prior expectations about its behavior: spikes tend to cause damage when you fall on them, coins are good things to collect, and the "king" and "queen" are likely valuable pieces. Sometimes our knowledge is transferred from the real world, but often it is also transferred from other games: learning the rules of Texas hold 'em is easy if you know the rules for five-card draw and the behavior of missiles in Space Invaders is similar to the behavior of missiles in Ikaruga. At a simpler level knowledge transfer also applies between different parts of the same game: big Goombas in world 7 likely have behavior that is similar to smaller Goombas in world 1. This idea of knowledge transfer between games based on prior experience, both from within the same game and from other games, represents one of the most fundamental ideas of general game learning and we will attempt to leverage it wherever possible when developing a game learning algorithm.
Learning from mistakes — Humans who are good at playing games can make rapid progress through games even if they are encountering them for the first time. Part of this success is achieved by borrowing from their considerable experience with other games in the same genre. Another indication of a skilled player is the ability to rapidly overcome challenging parts of a game by identifying the regions where they made mistakes and strategically planning a solution based on their experiences. For example, in Chess a player who loses to fool's mate is not likely to make the same mistake twice. In the case of games such as Mario, a player who is killed by a fireball shot from an enemy because they jumped too late is going to refine their timing on future iterations. The ability to identify and learn from mistakes is critical for developing an effective game learner. Mistake learning also allows us to quantitatively evaluate the quality of learners: one learning algorithm is more effective than another if it is able to learn from its mistakes using fewer examples.
Learning through conversation — Whenever possible many humans prefer to learn from other humans. Through conversation we can rapidly learn the rules of a game, have rules that we do not understand correctly pointed out and corrected, and ask questions about anything that confuses us. Humans can even provide feedback on more sophisticated reason patterns such as whether a rook is more valuable than a bishop in Chess. Unfortunately, at present computers cannot easily sustain meaningful conversations with humans. However, as described above humans can still be invaluable to general game learning by providing examples of game play. Humans might also provide feedback for a small number of computer playthroughs by annotating certain regions as good or bad. They might note that when Mario jumps into lava and dies this is bad, and when Mario advances to the next world this is good. A learning algorithm might in turn learn certain visible features that correspond to bad behavior, such as it is bad for Mario to touch spikes, and avoid these behaviors on future iterations.

Symbolic Representation

All learning tasks for all types of input start by first transforming the data into a form that is more suited for learning. When we process a visual scene such as a computer desk or a chess board our brains do not attempt to consciously process the set of raw activation energies in the rods and cones in our eye. Instead the visual signal is processed through a large series of sophisticated filters that perform tasks such as dominant edge extraction and object segmentation before finally reaching the conscious part of our brain. At some stage along this visual processing pipeline we recognize and categorize all the relevant objects we observe so that we can reason about the object's properties, the relationships between the objects, and how the objects are likely to react to various stimuli or the passage of time. In the context of games, for example, we likely start by breaking up an image of a chess board into an 8x8 grid of 64 board tiles, pieces such as "a white pawn", and assign each piece to one of the board tiles or note that they are "off the board" (captured). This separation into meaningful objects and categories allows us to map the problem onto an internal representation where it is possible to reason about the rules of the game. We also need to match the entities in the internal representation through time and in the presence of possible animations or deformations. Finally we need to remember certain properties of the game that are the result of past events in the game but are not explicitly visible from looking at the current state. We refer to this information as hidden state.

Humans have an impressive ability to independently arrive at fairly similar representations for games which enables us to easily communicate rules and strategies to each other. We know a representation is correct because it is reinforced by other knowledge sources such as the rulebook and because the correct representation enables us to easily predict how the game evolves with respect to time and the controls for the game. For example, if a game is composed of two dominant "ground" and "sky" regions, and due to complex texturing we accidentally think a certain region of pixels corresponds to the sky when in fact it belongs to the ground, we will rapidly correct our representation if we attempt to move our character through this region and find it to be impassable.

The process of constructing and updating an internal representation in response to observations and experience is fundamental to effective learning for both computers and humans. Computers must also transform the raw input signals into a symbolic representation before they can effectively reason about how to play the game, but enabling computers to map the raw signal to a useful internal representation is no easy task. Even if we restrict our analysis to two dimensions, real games have significant decoration, occlusion, animation, texture, and shading effects all of which make it very hard to determine what the relevant game entities are. Furthermore, computers do not have our intrinsic knowledge of concepts such as a game piece, a game board, a grid, or our ability to recognize objects such as a gun, spikes, or mushrooms. Trying to learn without these concepts is very challenging, but manually teaching the computer every single concept for each game is not general. Instead we will compromise and attempt to come up with a set of general patterns such as lines, boards, grids, pieces, maps, and parabolas. These convey relevant aspects of our general experience and knowledge that we start with when we approach a new game. We refer to these general concepts and patterns as concept templates, which we will discuss in more detail later. In addition to templates, we can also attempt to emulate the human behavior of updating our internal representation based on our experiences. By trying to learn rules using multiple possible segmentations of the game into entities, we can pick the entity decomposition that leads to the best understanding of the game. An internal representation model is good if it can correctly predict how the game evolves with respect to time and user input.

Related Work

The vast majority of existing artificial intelligence research for games focuses on AIs that are able to play a specific game well. Although such AIs are very specialized, this research is still important for general game learning because it gives us a good idea of what kind of algorithms might lead to effective strategies once we determine what the rules of the game are. General game playing is an attempt to generalize these game-specific AIs. It assumes that the rules of the game have already been learned and specified in a machine readable format. General game playing is a subset of general game learning and is invoked once the computer believes it has a reasonable understanding of how the game is played, and then needs to develop an effective strategy for playing the game. Several ideas important for general game learning have been studied in the context of general game playing such as knowledge transfer. Very limited work has been done on learning the behavior of entities in games through observation, one example being predicting computer behavior in the game of Pong.

A small amount of existing research has been done on general game learning coming from the perspective of robotics. The goal is to allow robots to learn the rules of a game by watching human observers. Because this is so challenging the space of games used are extremely restricted in complexity and have not yet exceeded the level of Tic-tac-toe or Hexapawn. At present the most developed research in this field is a paper from Purdue University called Learning Physically-Instantiated Game Play through Visual Observation. The games the robots play on are restricted to a 3x3 grid and take on a very specific form. The symbolic representation is hand-coded and classifiers are manually designed for the two types of pieces available, which are chosen to be easily disambiguated using computer vision. Despite being highly specialized and restricted, the robot is able to learn which permutation of the game is being played through observation and constitutes a real-world example of a general game learning system.

Pipeline

Above we have given a vague outline for the components that make up a general game learner. We now flesh out the stages of a complete pipeline that is modeled after the human approach. At a high level the algorithm's input is a video feed of a digital game and the output is a set of keyboard, mouse, and game controller events.

Extract symbolic representation — Given a video feed from the game, we want to extract a set of meaningful objects that capture the important entities in the images. We can then take a newly observed frame and acquire a symbolic representation for it. Because we cannot yet know which segmentation is correct, we extract multiple candidate symbolic representations and choose between them based on which is most successful at learning the game.
Determine valid actions — Given an input game state we need to decide what actions are likely to affect the game state and correspondingly the symbolic representation. For example, in Chess pressing the "y" button on the keyboard is not likely to have an effect, and clicking at <154, 122> is likely to perform the same action as clicking at <154, 123>. We need to try and quantize the actions to a meaningful subset of the complete space of possible controller inputs so that rule learning will be possible.
Learn a game model — Given a candidate symbolic representation and a set of possible actions we need to learn a set of rules that describe how the system evolves with respect to actions and time. A model is good if it is able to predict the observed changes to the game state.
Determine the goal — Once we have a model for how the game state evolves we need to try and understand the goal of the game. This is a very challenging task because there is no simple way to evaluate whether or not we have found the "true goal" of the game. However we can try to guess the goal by using heuristics such as novelty or trying to optimize visible integers such as the game score. We can also try to guess what attributes of the game the human is optimizing by watching the playthroughs.
Plan actions — Given a symbolic state, a set of possible actions, a game model, and a goal, we need to plan a set of actions that accomplish the goal.

These pipeline stages are not sequential. For example, we will need to update our symbolic representations when we encounter new areas of the game with behaviors and objects we have never before observed. Likewise, we might modify our symbolic representation if we find that it does not correctly predict the behavior of the game, or we might modify our goal if we find it does not seem to be effective at mimicking human behavior.

It should also be noted that this is hardly the only possible factorization of the game learning problem. An alternative learner, for example, would be to cast the problem as a supervised learning problem where the domain is the pixel values of the current screenshot from the game and the range is the correct output. Such a learner requires a large number of human playthroughs and is not likely to be effective on complex games but constitutes a useful comparison.

Below we go through each of the pipeline stages in detail. For each stage we will give examples using Tic-tac-toe, Chess Titans, and Super Mario Bros., which will demonstrate many different types of challenges faced by general game learners.

Stage 1: Extract Symbolic Representation

In this stage we extract symbolic representations from a set of video frames. These video sequences might come either from human playthroughs or through the learner's own attempts to explore the state space of the game. There are many viable approaches to extracting representations; the approach I use can be broken up into two stages: co-segmentation and template matching.

Co-segmentation — The purpose of this phase is to extract candidate template images from the input feed. A region in the image is a good candidate if it repeats many times at many different locations. This is called co-segmentation because the idea is to find dominant repeating patterns in multiple images. Computer vision has developed several algorithms for performing co-segmentation on two photographs, most of which cast the problem as solving a Markov random field. Directly applying a co-segmentation algorithm designed for photographs does not yield satisfactory results when used on game images, but it is possible to adapt the algorithms to give reasonable performance. The specific algorithm I based my GGL co-segmentation algorithm can be found here. The adaptations needed to handle the multi-class and multi-image case are somewhat significant, and although I have not yet published my modifications I plan to do so in the near future. By modifying the expected size of a template and various other parameters, a large number of possible template images are extracted.
Template matching — Once we have a template image we need to actually identify each occurrence of the template image in the video feed. This is a standard problem called template matching. I use a very simple convolution approach for this stage; other more advanced algorithms exist such as those used in OpenCV.

Tic-tac-toe

Here are some screenshots from a game of Tic-tac-toe, and several different templates that can be extracted:

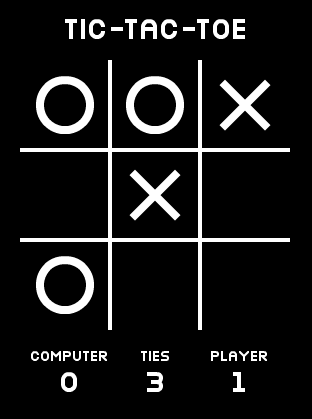
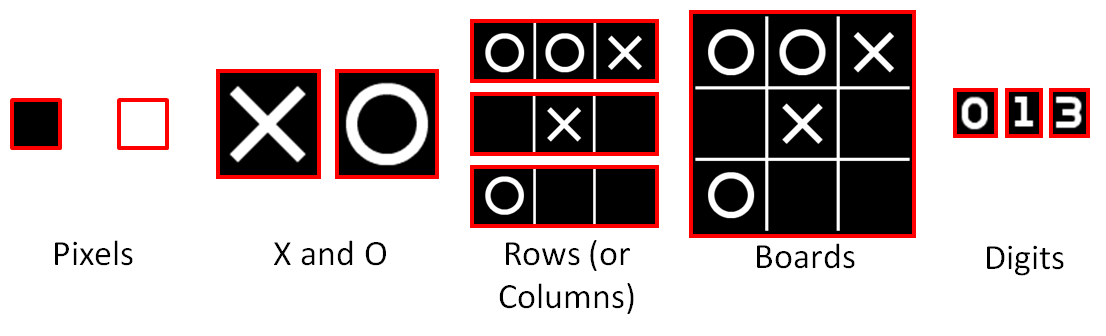
Many sets of these templates can be combined to provide a complete factorization of the game, and each would lead to a different symbolic representation. At the finest level, we might break the entire game up into pixels. There are only two colors, so this would result in a symbolic representation comprised of approximately 100,000 entities, each of which takes on one of two values. Clearly this is over-segmented. At a finer level, we can extract the "X" and "O" template which will lead to the standard representation used by humans. If we under-segment, we might group the pieces together into rows or columns. There are 27 possible templates in either orientation. Although such a representation is not used by most humans, it is still possible to form a reasonable set of rules. Finally, if we massively under-segment we might find each possible game board to be a possible template. For any interesting game, it will not be possible to learn rules using such extremely under-segmented templates.

The templates extracted from co-segmentation alone can be used to define a symbolic representation by enumerating for each frame the location and type of templates detected. However, such a representation often fails to miss necessary properties. For example, the grid structure is very important to Tic-tac-toe, because without it we cannot understand concepts such as an empty square or learn general rules about the victory conditions. Likewise, the template extraction might be able to extract the individual digits but does not understand the rules of counting or how an integer is represented as a base-10 string. Rather than expect the game learner to re-derive such general concepts, we explicitly teach it a set of concept templates that it applies to attempt to recognize common patterns across games. The two concept templates that are relevant to Tic-tac-toe are the concept of a N by M grid and the concept of a string being represented as a collection of digits. A grid is detected when sets of templates occur close to the vertices of a regular lattice. Digits are detected by looking at horizontal rows of templates of a certain size that occur at near-periodic spacing, and then attempting to run optical character recognition on the set of such templates.

After we extract all the entities from the image templates and apply the concept templates for grids and integers, we will get a large symbolic representation. Some subset of this representation will correspond to the human perspective of the game: a 3x3 grid with 3 possible entries, "empty", "X", and "O", and the three integers shown at the bottom.

Chess Titans

Extracting a symbolic representation for Chess Titans (shown here) will encounter many of the same problems as doing so for Tic-tac-toe, but on a larger scale. The desired representation is an 8 by 8 grid, each element of which corresponds to one of 13 possible values. However, in the process of extracting the desired image templates for these pieces, we are likely to capture many other templates corresponding to aspects specific to the Chess Titans interface, such as the colored regions indicating possible moves. These interface-specific indicators are very interesting from a learning perspective. On one hand the computer might find them distracting and they could complicate rule-learning. However, they could also be invaluable for learning the set of possible moves in the same way they might help a novice human Chess player learn the legal moves in Chess.

Super Mario Bros.

Here is a screenshot of Super Mario Bros. and parts of the corresponding tileset used to generate images in the game:

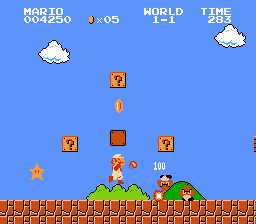
These tilesets are not what will be extracted using the co-segmentation algorithm above. However, because the case of tiled games is common I have a special algorithm for automatically extracting tile sets from games that appear to be largely tile-based. This tileset leads to a symbolic representation which is a collection of background tiles with some overlaid sprites such as our heroes and enemies. One interesting aspect of Super Mario Bros. is that there are natural clusters between some of these tiles that can be detected using simple visual comparisons. For example, without any processing there will be a large number of different sprites corresponding to the Mario character, each of which will be assigned a unique identifier. Because each of these sprites conveys potentially useful information such as whether Mario is jumping or running we likely do not want to collapse them all into a single entity. However, by detecting the similarities between these sprites we might be able to assist the rule learning stage later in the pipeline.

Note that we have ignored many other important cues besides the input video feed. For example, many games have important sound effects that let the user know when they have done something good or bad, or to signal an important event occurring in the middle of a game. These cues could be incorporated into the symbolic representation in a similar fashion by extracting repeating audio patterns and then added them in as symbolic events when they are detected.

Hidden State

The symbolic representations we have described thus far contain only information that can be learned from the current screen. To learn effectively we will need to capture several other properties that are based off the history of the game. For example, when we look at a Chess board we need to know which player is currently making a move, whether any of the kings or rooks have moved, and the previous few moves for the purpose of determining stalemates or en passant. One option is to consider the symbolic representation to be cumulative, and concatenate all information from the first frame through the current frame. This encodes far too much information to make learning useful, so instead we select only certain pieces of knowledge that depend on the genre of game. For example, if we detect a grid, we might add hidden state variables indicating whether each grid piece has been moved. Another important piece of hidden state is to annotate, for each entity, the coordinates of the closest entity of the same type in the previous few frames. This inter-frame correspondence is very useful for many types of games and allows the learner to predict the future motion of objects by learning rules about position and velocity.

Stage 2: Determine Valid Actions

In this stage we need to decide what actions are meaningful to the symbolic representation. We make a distinction between two types of actions: physical actions and symbolic actions. A physical action is applied directly to the game such as "click at coordinate 212, 517" or "move left analog stick to (0.30, 0.85)". A symbolic action is applied to the symbolic representation such as "move the piece at grid coordinate (2, 3) to coordinate (2, 5)" or "move the top card in pile 5 to the top of pile 6". Symbolic actions are important because these are the types of actions we reason about when we learn and play games. In this stage our goal is to learn what actions are possible from experimentation and by observing the human playthroughs. For learning and planning, we need a way to enumerate what physical actions are interesting and a mapping from each such physical action to a symbolic action. When we actually want to execute a planned symbolic action, we will also need a mapping from the symbolic action back to a physical action.

For some games, there is not much distinction between symbolic and physical actions and determining a set of viable actions can be easily accomplished by copying all physical actions executed by humans. For example, in Super Mario Bros., the controller only has eight digital buttons: "A", "B", "Start", "Select", and the four directional buttons. Using these physical actions as symbolic actions is likely to be sufficient for the purposes of motion planning and rule learning.

For other games such as Chess and FreeCell physical and symbolic actions are much more distinct because of the extremely fine discretization of inputs like the mouse. Attempting to copy the human actions is not likely to capture all possible moves, and humans do not always click in exactly the same locations so the same symbolic action may be duplicated many times. To overcome these challenges we rely upon our concept templates. Each concept template such as a button, grid, or stack has a list of relevant "symbolic locations". For example on a grid these might be the centers of each grid cell, and on a button would just be the center of the button. Each concept template that has been clicked on can contribute a set of symbolic actions, and the set of all such symbolic actions is used to quantize the possible click locations to meaningful actions. Keyboard and controller buttons are directly mapped to symbolic actions because these are typically small enough in number that the number of symbolic actions remains manageable.

In most cases the set of symbolic actions we acquire will be a superset of the meaningful ones. Most of the time, pressing "select" in Super Mario Brothers or typing "q" in Chess Titans might have no effect. Likewise in Tic-tac-toe, clicking on a grid location that already has a piece is not a valid symbolic action. The goal of this stage of the pipeline is just to acquire a superset of possible symbolic actions; we will try to understand which of these actions are "legal" or meaningful in the next stage.

Stage 3: Learn a Game Model

Learning the rules that govern a game is the core of general game learning. The transformation into the symbolic representation and the extraction of symbolic actions is just to enable this process. Given the current symbolic representation of the game and a set of possible symbolic actions, we need to predict the next symbolic state of the game as a function of the action taken and how much time has elapsed. Given such a model for the game we can plan out the consequences of various actions which will be necessary for trying to achieve the goal of the game. We want to find a general model that can represent most of the games we are interested in and can be learned from experience. If we use a model that is too general such as an arbitrary, Turing-complete language, we are likely to find the problem of learning the game model intractable. We can still make progress however because although most interesting games are very complex, this complexity usually arises through the interaction of relatively simple behaviors. While we cannot hope to reverse engineer all of the programming behind Super Mario Bros. from observations, if we focus on only a single part we will often find it simple enough to model. For example, below we show three frames of motion from Super Mario Brothers 3, which can be used to estimate the fairly simple motion model for Goombas. We will attempt to build our model as a series of smaller parts by learning rules that define a small aspect of gameplay. We want to define rules that can be parameterized to capture most of the important behavior in games without being so specialized that new rules must be designed for every possible game. They also need to be sufficiently concise to permit searching through the possible set of rules to find those that best explain the observed evidence.

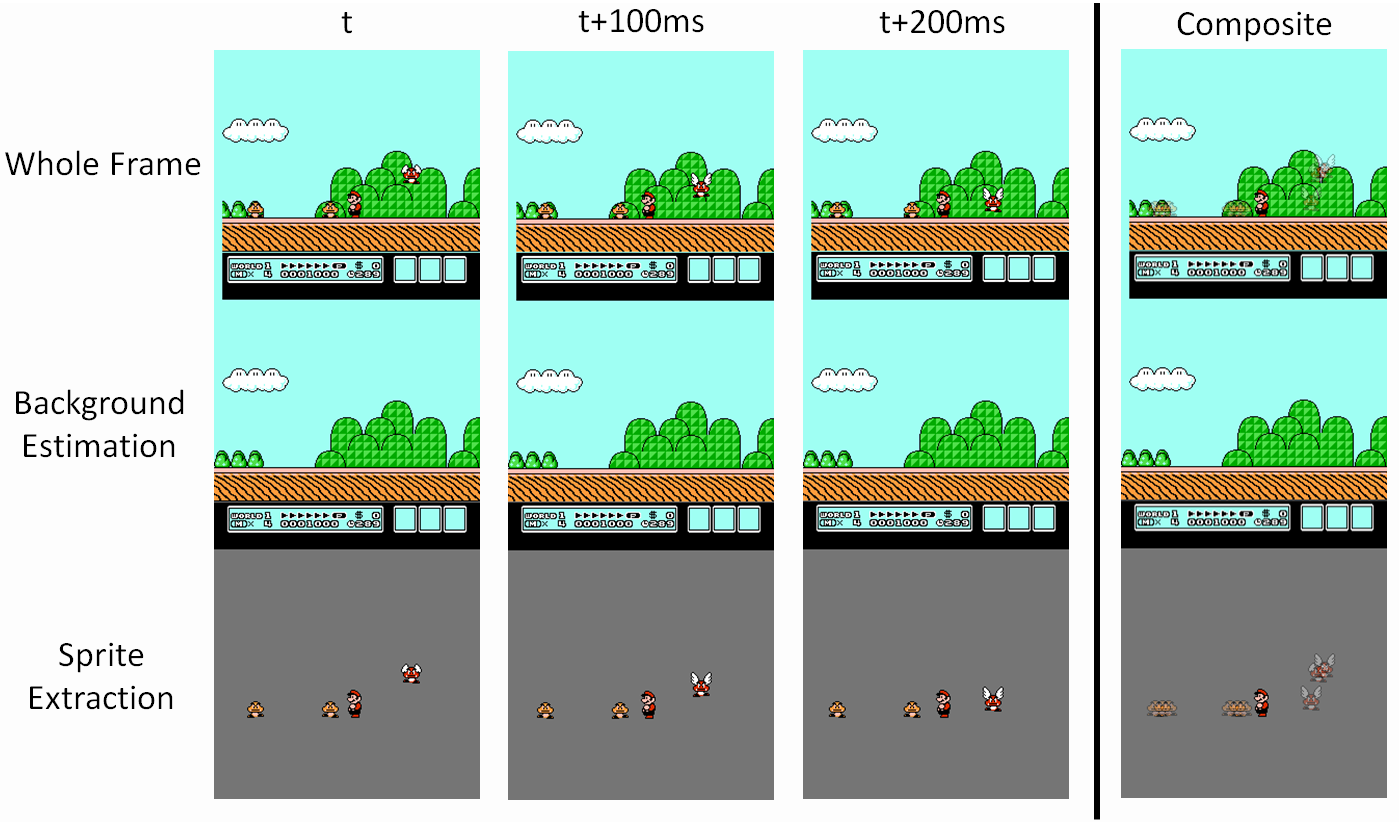
Humans use natural language to describe rules. The vocabulary we use is very specific to the type of game and many games will define entirely unique vocabulary such as "check" in Chess. We can define an analogous set of rules in a formal language for games, which will likewise use genre-specific vocabulary so that the rules can be concisely defined. Before we do so however, we will try to enumerate a few rules for several games using natural language to get a feel for what the formal language might look like.

Tic-tac-toe

The game starts with all pieces on the board empty and the three counters all zero.
If a line is formed with three pieces of the same type, then the current player wins, the appropriate counter is incremented, and the board is reset.
If the board contains 9 pieces and no one has won, then the "ties" counter is incremented and the board is reset.
The active player switches each time a move is successfully made.
When the game is reset the player who went second last game starts this game.
If you click on a square that already contains a piece, or if you click off the board, nothing happens.

Chess

A player cannot move pieces if it is not his or her turn.
It is not legal for a player to move a piece into a square occupied by a piece of his or her color.
A player can move a rook along any horizontal or vertical straight line so long as the intervening pieces are all empty.
It is legal for white player to move a white pawn forward two squares if it is in its home row and the square in front of the pawn is empty.
It is not legal to move a piece if doing so allows your opponent to take your king on his or her next turn.
If the cells between a rook and a king are all empty and neither the rook or king have moved then you can perform a castle, where the kind moves two spaces towards the rook and the rook moves into the first empty space that the king moved through.
A player loses the game if they do not have any available actions which can prevent the opponent from capturing their king on the following turn.

Super Mario Bros.

Pressing right moves Mario to the right.
Pressing A causes Mario to jump.
Goombas move slowly in one direction and can fall off ledges. If they hit an obstacle they will flip directions.
If Mario falls into a pit or fire he will die.
Jumping on Goombas kills them but colliding with them from the side will hurt Mario.
When you jump on a Koopa-troopa it will turn into a shell. If Mario collides with a shell it will start moving away from Mario quickly. The shell will kill enemies it comes into contact with and will bounce off obstacles. The shell can also fall off ledges.
When Mario reaches a flag at the end of a stage he advances to the next stage in that world.

We will try to make our computer-targeted rules capture similar concepts to the rules given above. These natural language rules offer several insights into what kinds of properties machine-readable rules might need to concisely describe games:

Categories — Many rules refer not to an individual entity such as "a white pawn" but to whole categories of entities, for example the rule "white player can only move white pieces". Although this rule refers to the set of white pieces, our algorithm has no way of knowing beforehand what this is; all the computer knows is that there are 12 different entities each with a unique identifier. The "white pieces" category repeats in many other rules as well, such as "white player cannot move pieces onto squares that contain white pieces". To capture this behavior, our rules will manipulate sets of categories as first-order objects and attempt to generalize specific information to general categories as aggressively as possible. For example, suppose we have identified that a set of entities corresponding to the six white piece types is important. If we then deduce the rule "white player can move white pawns" and "white player can move white queens" then we might consider the rule "white player can move white pieces" since "white pieces" is a category that contains two elements for which the general rule holds. Although such aggressive generalization may be wrong, in the process of playing the game under such incorrect generalizations the learner will inevitably encounter counter-examples to its incorrect beliefs that will force it to refine its categorizations. This ability to rapidly stereotype is critical to effective learning.
Factorization — The rule "white player can only move white pieces" and "black player can only move black pieces" have the same structure. To unify them, we might instead say "each player can only move their own pieces". Whenever we detect several rules that each take an identical structure, we will attempt to unify them by factoring out the common structure. Similar to stereotyping objects into categories, we can look for the same types of factors being repeated across different rules.
Strong typing — Another property of natural language rules is that there are many different genre-specific types used such as "players", "pieces", "cell", and "board locations". We will also make use of a type system to define our rules. We want to construct a set of types that is sufficiently powerful to capture the rules of the games without being too specific that it cannot generalize between games. Typing is beneficial for permitting efficient searches through the space of possible rules to find those that best explain the evidence.

Game Model Language

A natural starting point for a game model language might seem to be existing languages that have been used to describe games such as the Game Description Language (GDL). Using this specification we could then apply inductive logic programming to learn the game model, as has been done for the robotic general game learners. This is certainly one option for developing a game learner and would be interested to explore. The difficulty with GDL is that the resulting rule sets are often very verbose and challenging for both humans and machines to understand; for example, the rules for Checkers are hard to follow and likely far too complex for inductive logic programming to derive a meaningful set of rules. Although we do not need our rules to be human-readable, constructing a set of rules that is similar to the human way of defining game rules enables us to more effectively borrow human techniques for strategizing about effective gameplay. More importantly, transferring knowledge between games is greatly facilitated when the games are expressed in a similar, typed language. The typeless nature of GDL means that it is very hard to understand which parts of the rules governing "Super Mario Brothers 1" might be transferred to "Super Mario Brothers 3", which is one of the key goals of GGL.

Different genres of games require very different types of reasoning and draw upon different parts of our experience. Our knowledge of the rules of physics are useful for understanding Mario, but provide little benefit when playing Chess. We will encode general human knowledge by providing our language with basic functions such as the concept of straight and diagonal lines on a grid and a quadratic model for predicting motion. For the purposes of this tutorial, our goal is not to formally specifying a language sufficient to encompass all interesting games, as that is one of the core research areas of GGL. Instead we will sketch a toy genre-specific language corresponding to piece-type games such as Tic-tac-toe, Chess, Checkers, and Othello; this language is not complete by any means, but will allow us to investigate many important GGL topics such as knowledge generalization and category formation. Throughout this section we will often use names for entities such as "whitePawn" or "whitePlayer" which suggest that our algorithm has some prior knowledge about the similarity between categories or some other means of describing them. This is not at all the case, and to the computer these would be represented as something like "entity6" with an associated image template. We only use human names in this section to help make the examples more clear.

Basic structure — The language is strongly typed and uses a simple functional style. Every expression is either a terminal symbol with a single type, or a function with fixed arity and each parameter takes a single pre-defined type. There is no implicit conversion of any kind or any form of operator overloading.

Primitive types — Each piece-type game is expected to have a single grid that has been identified during the symbolic representation stage. The primitive types our language will use to refer to this grid and the pieces on it are: bool, int, player, action, effect, coord, coordSet, pieceType, pieceTypeSet. An effect is a consequence of a player executing an action. A coord is a pair of integers corresponding to a specific location on the board. A coordSet is an unordered collection of coordinates. A pieceType is a specific type of piece such as "whitePawn", and a pieceTypeSet is a collection of such pieces such as the set of all white pieces in Chess. "empty" is a special piece type that exists for all games with a grid and denotes a grid cell with no detected image template.

Functions — Here we show some of the basic functions that are part of the language:

bool and2(bool, bool), bool or2(bool, bool), bool not(bool) — Basic boolean "binary and", "binary or", and "not" expressions.
int add2(int, int), int subtract2(int, int), int multiply2(int, int) — Basic integer operations.
pieceType pieceAt(coord) — Returns the type of piece currently at the given coordinate.
int countPieces(pieceType) — Counts the number of pieces of the given type anywhere on the board.
bool coordContainsPieces(coord C, pieceTypeSet P) — Returns true if the board location specified by C contains a piece that is a member of P.
bool coordSetContainsPieces(coordSet C, pieceTypeSet P) — Returns true if all of the board locations specified by C contain pieces that are members of P.
coord lineDirection(int Direction) — An index into one of eight compass directions on a grid (see diagram below). For example lineDirection(2) returns (1, 1).
coordSet line(coord Start, int Length, int Direction) — Returns the set of coordinates in a line whose origin is Start. Length is the number of elements in the line and Direction specifies which of the eight cardinal directions the line travels in.
action click1(coord C) — This action presses the mouse at the center of the grid location specified by C. It is meant for games such as Othello where a single piece is placed.
action click2(coord C1, coord C2) — This action first clicks at the center of the grid location specified by C1, followed immediately by clicking at the center of C2. It is meant for games such as Chess where a piece is moved from one location to another.
effect assign(coord C, pieceType P) — An effect that assigns the type of the piece currently at C to be P.
effect concatEffect(effect E1, effect E2) — Combines two effects by first executing E1, then executing E2.

Here we visualize the meaning of the Direction parameter for the lineDirection and line functions:

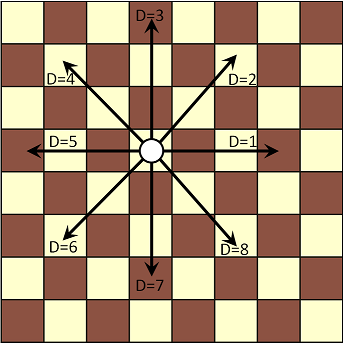
Rules — Rules are special expressions that are defined by a specific set of types that specify properties such as what the next board state will be and what actions are legal. These are analogous to the legal, next, does, terminal, and goal keywords in GDL.

legal(player, action, bool) — If the boolean expression is true, then it is legal for the player to take the specified action.
notLegal(player, action, bool) — If the boolean expression is true, then it is illegal for the player to take the specified action.
does(player, action, effect) — If the player takes the specified action, then the given effect occurs.
terminal(bool) — If the boolean expression is true, this is a terminal state signaling the end of the game.
score(player, int) — If this is a terminal state, then the score for the player is the given integer.

The functions and rules listed above are sufficient to specify the rules of a large number of games. We will first demonstrate how they are capable of encoding such rules, and then discuss how we might go about learning them from observations. One problem with our current rule description is that by themselves, these rules have no potential for generalization. To see this let's look at a rule for pawn advancement in Chess (board coordinates are numbered from 1 to 8, column coordinate first):

legal(whitePlayer, click2(coord(1,2),coord(1,3)), and2(coordContainsPiece(coord(1, 2), whitePawn), coordContainsPiece(coord(1, 3), empty)))

In English, this rule says "it is legal for white to move a piece from (1, 2) to (1, 3) if (1, 2) contains a white pawn and (1, 3) is empty." Because this prefix-like notation for writing rules can be harder for a human to parse, we will switch to a C-style infix notation from now on, and use ∈ as shorthand for the coordSetContainsPieces-type functions:

legal(whitePlayer, click2(coord(1, 2), coord(1, 3)), coord(1, 2) ∈ whitePawn && coord(1, 3) ∈ empty)

Although this rule is true, it is a far more specific rule than a human would use to describe the game. This rule in fact holds for many other locations on the board. To support such generalization we will create a local variable X that indicates the current row for which the rule holds. We then specify for what values in the domain of X the rule is true. In logic, this notion is called quantification and we will use a notation for it that is reminiscent of the use of generics or templates in many programming languages:

<int X[1,2,3,4,5,6,7,8]> legal(whitePlayer, click2(coord(X, 2), coord(X, 3)), coord(X, 2) ∈ whitePawn && coord(X, 3) ∈ empty)

This template notation can be interpreted as being eight rules, one for each possible value of X. The values inside [...] provide a list of the valid values of the domain of X and must all be of the appropriate type. We will use 1→8 as shorthand for the integers 1 through 8.

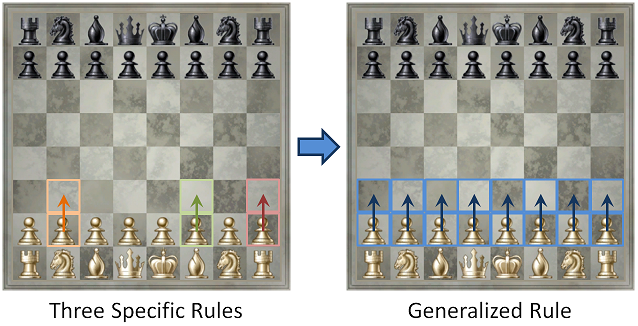
This rule generalizes the pawn-advancement rule for the entire home row, but this rule also holds for many other rows. To support this we will add another template parameter; a multi-parameter template expands as the complete product of all its parameters. So the general rule looks like:

<int X[1→8], int Y[2→7]> legal(whitePlayer, click2(coord(X, Y), coord(X, Y + 1)), coord(X, Y) ∈ whitePawn && coord(X, Y + 1) ∈ empty)

This rule now generalizes across all rows and columns and is much closer to the pawn-advancement rule used by humans. Because this is a very common case in board games, we will go one step further and define a special template parameter board which is a domain for a coordinate variable that spans all possible grid locations. Although it is not possible for white to have a pawn in row 1, such generalization will not affect the ability of a computer to reason about the game rules. So the final pawn-advancement rule is (here we use simple component-wise coordinate addition):

<coord P[board]> legal(whitePlayer, click2(P, P + coord(0, 1)), P ∈ whitePawn && (P + coord(0, 1)) ∈ empty)

Given this notation we can easily specify many other Chess rules. We cover several such rules below:

Pawn home-row advancement	<int X[1→8]> legal(whitePlayer, click2(coord(X, 2), coord(X, 4)), coord(X, 2) ∈ whitePawn && coord(X, 3) ∈ empty && coord(X, 4) ∈ empty)
Pawn attack	<coord P[board], coord D[(1, 1), (1, -1)]> legal(whitePlayer, click2(P, P + D), P ∈ whitePawn && P + D ∈ blackPieces)
Knight move	<coord P[board], coord D[(1, 2), (1, -2), (-1, 2), (-1, -2), (2, 1), (2, -1), (-2, 1), (-2, -1)]> legal(whitePlayer, click2(P, P + D), P ∈ whiteKnight)
King move	<coord P[board], int X[-1→1], int Y[-1→1]> legal(whitePlayer, click2(P, P + coord(X, Y)), !(X == 0 && Y == 0) && P ∈ whiteKing)
Bishop-side Castle	legal(whitePlayer, click2(coord(5, 1), coord(7, 1)), coord(5, 1) ∈ whiteKing && coord(6, 1) ∈ empty && coord(7, 1) ∈ empty && coord(8, 1) ∈ whiteRook)
Rook and Queen move	<coord P[board], int N[1→7], int D[1, 3, 5, 7], pieceType piece[whiteRook, whiteQueen]> legal(whitePlayer, click2(P, P + lineDirection(D) * N), P ∈ piece && line(P, N - 1, D) ∈ empty)
Bishop and Queen move	<coord P[board], int N[1→7], int D[2, 4, 6, 8], pieceType piece[whiteBishop, whiteQueen]> legal(whitePlayer, click2(P, P + lineDirection(D) * N), P ∈ piece && line(P, N - 1, D) ∈ empty)
No self-capture	<coord P1[board], coord P2[board]> notLegal(whitePlayer, click2(P1, P2), P2 ∈ whitePieces)
Consequence of moving	<coord P1[board], coord P2[board]> does(whitePlayer, click2(P1, P2), assign(P2, pieceAt(P1)) + assign(P1, empty))

These rules define many of the allowed movement behaviors for Chess. This is hardly the only possible way to group the rules of Chess; for example, the "notLegal" expression could be removed and something like "&& P2 ∉ whitePieces" appended to each of the "legal" expressions. The ability to factor out the common sub-expression permits learning smaller rules, however it also requires us to define an ordering on our rules to determine which statement has priority. Although these rules demonstrate considerable generality, as stated they all work only for white player. We will need an additional type of notation to permit us to generalize some rules for both players:

No self-capture for white	<coord P1[board], coord P2[board]> notLegal(whitePlayer, click2(P1, P2), P2 ∈ whitePieces)
No self-capture for black	<coord P1[board], coord P2[board]> notLegal(blackPlayer, click2(P1, P2), P2 ∈ blackPieces)
No self-capture	<coord P1[board], coord P2[board], {player activePlayer, pieceTypeSet pieces}[(whitePlayer, whitePieces), (blackPlayer, blackPieces)]> notLegal(activePlayer, click2(P1, P2), P2 ∈ pieces)

The phrase {player activePlayer, pieceTypeSet pieces}[(whitePlayer, whitePieces), (blackPlayer, blackPieces)] means "this rule is true when activePlayer is whitePlayer and pieces is whitePieces. It is also true when activePlayer is blackPlayer and pieces is blackPieces". The {...} defines a structure, in this case a pairing between a player and a pieceTypeSet, and the values inside [...] indicate possible values that the memebers of this structure can take. This is distinct from <player activePlayer[whitePlayer, blackPlayer], pieceTypeSet pieces[whitePieces, blackPieces]> which would imply that white cannot capture black pieces and that black cannot capture white pieces.

Chess is a fairly complicated game, so it is good that our language is sufficiently expressive to capture many of its rules. We will not spend much longer demonstrating the ability of this toy game language to describe game rules, but just to provide a different game example we will give a few rules for Reversi (also known as Othello):

Line Formation	<coord P[board], int N[1→7], int D[1→*8]> legal(whitePlayer, click(P), P ∈ empty && line(P, N, D) ∈ blackPiece && P + lineDirection(D) (N + 1) ∈ whitePiece)**
Termination	terminal(countPieces(whitePiece) + countPieces(blackPiece) == 64)
White Score	score(whitePlayer, countPieces(whitePiece))
Black Score	score(blackPlayer, countPieces(blackPiece))

Although this language is sufficient to represent and generalize many rules of certain types of games, there are many other important types of generalizations that are possible but that we will not discuss; the purpose of this language is just to explore some of the ideas of learning a game model. One such important concept is factoring out subexpressions that commonly occur in rules into general functions. This can both help with keeping rules concise and with searching over the space of rules. Likewise, many piece-type games such as Chinese Checkers occur on regular structures that are not grids. A more general language would generalize to learning rules over any graph structure. There are many other properties of piece-type games that would need to be modeled, such as Chess programs that use of a dialog box to select what piece type to promote a pawn to.

While it is necessary that a game model language be sufficiently expressive to efficiently encode the rules of a game, this is only useful if it is also possible to build a list of such rules from observations. This task can be broken down into two important questions: how do we efficiently search over the space of possible rules, and how do we determine whether a rule is good? Since the language is strongly typed enumerating the space of all rules of a given length is possible if the rules are sufficiently concise. By using techniques from inductive logic programming we can intelligently prune unlikely rules as we search through the space of possibilities to permit us to search for longer rules. Of course, the general task is undecidable, so we will never be able to guarantee the success of any such search algorithm.

To decide whether a rule is useful there are several simple heuristics that can be used, such as accepting a rule if it is usually true and helps explain the evidence. Although the best methods to decide when to accept rules can only be determined through experimentation, a clear starting point is to accept a new rule if it has high information gain, which is a metric often used in machine learning problems such as constructing decision trees. Another powerful heuristic is Occam's razor: because games are designed to be easily explained to humans, short and intuitive rules are more likely to be true than long, complex ones. Once we start accumulating a candidate set of rules, we can attempt to generalize them as demonstrated above by searching for sets of rules with common structures and factoring out the components that differ into free variables with an associated domain for quantification.

This language uses many concepts such as the notion of a legal move and a terminal state. These are common to many piece-type games but are essentially meaningless in other genres such as side-scrolling platformer games like Mario, where any action is legal at any time. To define the rules of Mario we would instead need new concepts such as the ability to specify how an object responds as a function of its environment. For role-playing games we might need a concept of a spatial map to determine where we have been in the world. Although these games are quite different from piece-type games, there are still some common aspects: both Mario and Chess have a notion of effecting the game state as a function of player action. Determining what properties of games are common across genres is one of the goals of general game learning research.

It may seem as if we will never be able to learn all the rules of a complex game through exploration. For example, even if the AI manages to learn that castling is possible, it is unlikely it will understand the specific conditions under which castling is impossible (cannot castle through check, cannot castle if either piece has moved). Doing so would require an incredible amount of training data because comparatively few games will encounter this situation. This does not defeat the concept of GGL however: precisely because these situations are relatively rare, it is possible to play a game effectively without understanding these rules precisely. Rules that are critical, such as the fact that a bishop can move along diagonal lines, are extremely common and consequently the most easily learned. In order to learn challenging rules, human playthroughs can explicitly attempt to encounter such situations to better teach such fringe behaviors of the game. Similarly, when the AI is learning the game model it can seek not to win the game, but to explore parts of the game it does not understand and recreate situations it has observed but that its rules do not correctly predict.

Stage 4: Determine the Goal

In the toy game model language we described above, there is a "terminal" and "score" expression that defines when the game is over and how "happy" each player is with each possible ending. This is certainly a convenient property for a game model to have, but unfortunately learning it is extremely challenging. Knowing how the game evolves offers little insight into what its objective is: Giveaway Checkers is a (surprisingly interesting) game that is identical to Checkers in every way, except that the winner is the first person to lose all of their pieces. When learning rules for how the game state evolves with respect to actions or time, it is possible to quantitatively evaluate how correct a rule is by seeing how well it predicts the observed changes in the game, but there is no straightforward quantitative recourse for learning the goal.

Fortunately all is not lost: games share many common properties and often have some observable clues to indicate success or failure. The easiest way to attempt to learn the goal is to use a supervised learning approach where certain regions of a human playthrough are annotated as "good" or "bad". The algorithm then analyzes these regions to try and understand what good or bad means. For example, here are some ending screens from a variety of games for the Nintendo Entertainment System (NES):

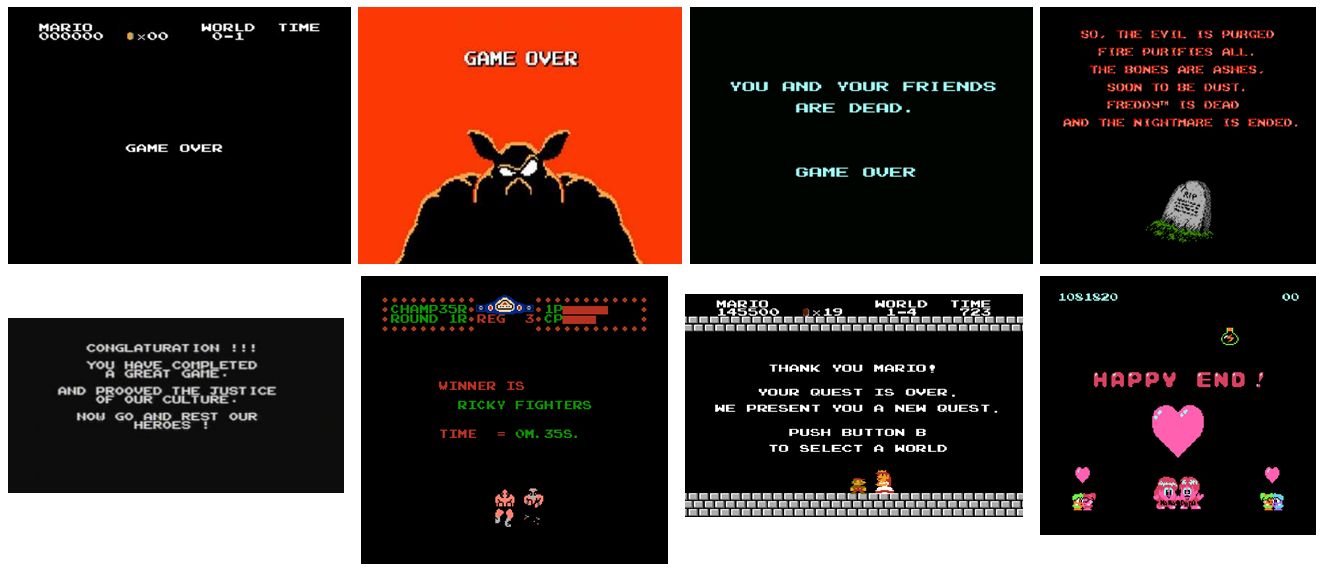
Analyzing these screens we might learn that phrases such as "dead" and "game over" are bad, and "thank you", "happy", "winner", and "conglaturation" are good. These properties are very interesting because they might generalize across many games, even games of very different genres. More practically, the game might be annotated at a much finer level: in Chess, the player might annotate moments where they captured the enemy queen as very good and where they lost their own queen as very bad, instead of only annotating the "final" outcome of the game.

Even without annotations we can still attempt to learn the goal. Games are universally meant to be fun and to be enjoyed. Sitting around doing nothing is not likely to be the goal of the game, and experiencing new and novel parts of the game, in addition to helping develop the game model from Stage 3, indicates progressing to new areas which is very likely to be making progress towards the goal. Indeed, the objective of a large number of platform games for consoles such as the NES and SNES can be summarized as "proceed to the right, and don't die." Just by exploring novel areas of the game and avoiding "boring" areas the AI is very familiar with (such as the death screen) the AI may inadvertently stumble upon the objective of the game: although without any external stimulus the AI will have no idea it has done so.

Novelty is correlated with the goal in many single-player games, but it is not going to lead to an effective AI for games such as Checkers. In such cases and in the absence of any user annotation, there is still hope. In competitive games, the evaluation function is a value assigned to each game state by an AI that is used to approximate how desirable the state is. By watching a user play, even if we do not know what moments of the play were good or bad, we can still attempt to approximately model the objective function they are using. For example, we might observe that in Chess the white player is attempting to capture black pieces. This is not the true objective of Chess — it is simply a means to more effectively capture the King. Nevertheless, even if we do not learn the true objective, modeling the intermediate objectives can lead to an effective AI. This is similar to the tactic used in the design of the evaluation function for Deep Blue where the function was broken down into approximately 8,000 parameters, which were tuned by observing grandmaster games. An exciting research area of general game learning is to attempt to reverse-engineer the evaluation function of another player from observations, and attempt to generalize such knowledge across games. This approach also applies to other genres such as platformer games where we might learn, through observation, that the player prefers to jump on the heads of enemies rather than be killed by them. A large number of games such as the Tic-tac-toe example given above and the games shown below have on-screen score counters, or list the number of lives of the player and their current health, all of which we might learn to be related to the game's goal.


Tetris	The Legend of Zelda	Desktop Tower Defense

Stage 5: Plan Actions

At this stage we can take a screenshot of the game, break it into symbolic entities, recognize common structures such as text, numbers, and grids, have some understanding of the rules of the game, and have a guess as to what the goal is. We now need to plan a strategy that accomplishes the goal by executing actions, which is the objective of conventional game learning and has a rich body of prior work we can invoke. In its full generality, this problem is a direct application of concepts such as the minimax rule from game theory for competitive games or reinforcement learning for agent-type games (such as Mario). However, directly applying some of these ideas, such as attempting to model Super Mario Bros. as a Markov decision process, is intractable due to the complexity and number of dimensions in the state space.

Fortunately, if we have any human playthroughs of the game we might already have a head start on action planning if we were able to approximate a value function during the goal learning stage. If we have such a function then we can directly apply the minimax algorithm or other planning algorithms to search for a path through our game state model that has high value according to the learned evaluation function. We then choose the best symbolic action in this space, convert it into a physical action, and execute it. Learning which algorithms work well for which type of game in the presence of complications such as an incomplete game state model is one of the research objectives of GGL. For example, if the AI has two options, one with medium reward and a very reliable state space model, and one with high variance according to the reward function but the AIs model of the game down this path has historically not been very effective at predicting future game states, what is the best way to decide which direction to proceed?

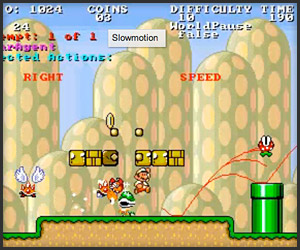
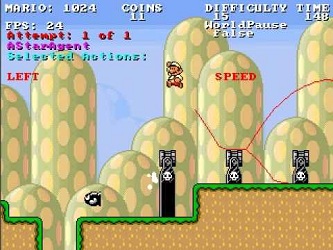
Even if heuristics such as novelty are not effective and we do not have a value function learned from human playthroughs, if we know the goal of the game this stages falls under the problem domain of general game playing and we can directly apply techniques from this field. Many approaches that have been successful at general game playing include extensive game simulation and bandit-based Monte-Carlo planning. General game playing has a yearly competition held as part of the AAAI conference where general game players compete using games written in the Prolog-like Game Description Language. This has resulted in a large number of successful and well-tested general game players, and it is certainly possible to convert a general game learner's game state model into GDL and invoke an existing game player. These general game players assume that the game model is perfect, so as in the case of evaluation functions learned from observing humans there is likely significant research to be done on incorporating game model uncertainty into the general game player. It should also be noted that in practice, most of the games written in GDL are variants of piece-type games and it is not likely that they could handle tasks such as playing The Legend of Zelda or Super Mario Brothers as these games do not efficiently translate into GDL. For such games, organizations such as the Mario AI Competition have been developed that explore ways to write effective controllers for platform games. The screenshots below shows various paths through the game a controller for this competition is considering.

Putting it All Together

At this point we have a complete set of stages that can attempt to learn any new game. Although there is some notion of ordering (we cannot attempt to learn how the game state evolves until we have extracted the game state from the video feed) it is unlikely that any stage will ever be "completed". The state space of an interesting game is so large that it is unlikely the exact same game state will occur multiple times, and we will constantly need to be testing and updating our likely incomplete model of the game space. Even though no stage is ever completed, depending on the game the objective of the general game learner may change over time. In the beginning the game learner likely has little idea how the input images should be segmented or what the rules that govern the game are. In this stage the learner places high emphasis on randomly exploring the game's state space as its understanding slowly improves. As time goes on the symbolic state will become more refined and the rules will be more predictive, and consequently more emphasis can be placed on matching the value function of observed players or attempting to match general objectives such as novelty. The transition between "random exploration" and "objective-only goal planning" is not a sharp one: in the act of more intelligently playing the game it is likely that new, unexplained areas of the game will be encountered that will require considerable exploration before further progress can be made.

There are a variety of exploration techniques that can be employed to learn to play games. The simplest exploration technique is "take a random action", but trying to understand a game by randomly mashing the keyboard and clicking all over the screen is not likely to be effective. A more intelligent exploration technique is to match the current game state against a list of human game states and take the action performed by the human. This is a useful technique because it can be done even before a reasonable evaluation function is learned (although it does pose the interesting question of how to compare two game states). For games such as Chess with a strong notion of legal versus illegal moves, it can be challenging to test a game model: the fact that the moves you predict are legal are observed to be legal moves says nothing about how many other legal moves you dismissed as illegal. One approach to overcome this problem is to explicitly test the game state model and attempt to perform all possible illegal actions and observe if any turn out to be legal. Of course, this is likely to be very slow: on an 8x8 grid there are 4096 possible two-part moves, suggesting a learner would benefit from an intelligent approach to selecting which moves to test. Determining which exploration approaches are most effective remains an open problem.

Evaluation

The ultimate goal of general game learning is to develop an AI that can take a novel game and, in a fully unsupervised manner, learn a model for the game and how to play it effectively. This is a compelling application because even if we restrict ourselves to 2D games there are literally tens of thousands of possible games spanning a variety of media such as console games, PC games, web browser games, and mobile games. This is a massive amount of information and such a dataset might prove sufficiently expansive to observe highly sought-after AI phenomenon such as knowledge transfer in real situations. As described earlier, an effective game learner is also exciting because many real tasks such as cleaning a room, emptying the dishwasher, paying your bills, or performing SQL injection attacks can be expressed in a game-learning framework.

Developing an effective game learner is a rich area of future research. One of the first tasks is to define what effective means. To test a game learner, a virtual machine needs to be specified that defines exactly what inputs the game learning problem takes and allows the AI to play an arbitrary game. Such a virtual machine might be connected to any number of game media, such as a software emulator for a video game console, which would allow it access to a large number of games that would provide reproducible and controllable gameplay to the AI. We have largely sketched what kind of information the AI has access to above such as the ability to observe the current screen, execute actions, observe human playthroughs, and obtain supervised feedback on the playthroughs. Using such a VM we can test a learner's ability as a function of game type by measuring how well it achieves certain objectives (which may be hidden to the learner). In this way, even in a fully unsupervised case, we might for example determine that the learner successfully beat the final boss, even though the learner was not aware that doing so was important. There are a variety of metrics that might be applied to test each stage of the pipeline, such as the percentages of moves in a board game that are correctly classified as legal or illegal based on the current set of rules, or the number of entities that it correctly predicts the motion of in a platformer game. By having many different games of many different game types we can observe how important GGL concepts such as knowledge transfer and learning human evaluation functions depend on properties such as game genre or the number and types of user playthroughs provided.

Each stage of the general game learning pipeline sketched above is very challenging and error prone. One use of such a virtual machine is that it can internally maintain a notion of the "correct" solution to each stage to permit efficient testing of the various components in isolation. For example, it can maintain a decomposition of a rendered game frame into sprites, which often correlate with a meaningful symbolic representation. Alternatively it might have a symbolic mapping directly provided from the original game, which could be invaluable for games such as Chess where the precise decomposition is very important for effective rule learning. This "ground truth" representation could be used to evaluate how effective an algorithm such as co-segmentation is at extracting meaningful entities from images, or it could be used to test effective rule learning without worrying over the inaccuracies introduced by the symbolic representation extraction stage. Allowing each stage to be tested in isolation is important since a complete pipeline is likely to struggle to learn a meaningful model of the game.

Although humans may take a while to develop skill with a game, we rarely require many attempts to understand the rules. General game learners, on the other hand, will likely take many hundreds or even hundreds of thousands of tries through a game to develop a general model. Exploring ways to learn efficiently and thus reduce the number of tries it takes to develop a game model is an important GGL task, but a virtual environment permits us several novel avenues. For example, we might allow the AI to revert to a previous time to explore a state that it had considerable trouble with, such as returning to the beginning of a boss fight without requiring it to defeat the whole level from scratch. If the AI was able to use this feature effectively it would likely result in considerably faster game learning.

The human brain is extremely fast at processing and understanding images, breaking them into entities and categories, and developing a model for how they evolve and react. A large portion of our brain is devoted to the visual cortex and reasoning centers of the brain, even a small component of which are dramatically more powerful than a fast computer. Thus it is unlikely that we can expect general game learners to be able to perform learning in real-time in the near future; the focus of GGL is on the ability to learn at all. Nevertheless, maximizing the amount of information learned from each frame and from each attempt to play a game will naturally lead to faster learners.

Although we have sketched a pathway for general game learning, any system which can effectively take meaningful actions when presented with an unknown game can be said to be an effective learner regardless of the method used to decide these actions. For example, a supervised learner might attempt to use the human playthrough as a training set to directly learn the best action given an input image, and such a learner might prove to be an interesting baseline for GGL. A good analogy is the DARPA Grand Challenge, where autonomous vehicles compete to navigate around unknown environments. It does not matter how these systems function internally, only that they successfully accomplish the goal. Still, it is no surprise that the different teams developed systems that solve the navigation problem in similar ways and thus share many common components that can be interchanged and independently evaluated. In GGL, for components such as the internal representation of the game model, there is no need for different learners to agree on some "common, universal game model language" the way there is for general game playing: it is not even clear whether or not different humans use an indentical model for a game's behavior.

Deliverables

We have mentioned a wide array of research goals for general game learning. It is also important to have specific questions in mind that provide useful insight into the problem. Below we list a small subset of the types of questions that might be investigated, categorized by research topic:

General

What types of games are hard to learn? What types are easy?
Do we learn symbolic representations that are similar to humans? Can we still learn the rules even if they aren't the same?
Is the number of frames it takes to learn a good metric of the game's complexity?
If we have two Chess programs, how quickly can we realize that they are equivalent?
We give a learner access to 199 NES games and measure how quickly it learns NES game #200. How much faster is this than giving the learner only game #200 in isolation?
Can we make a walkthrough or speedrun video of a game?
Can an expert computer learner make a series of effective playthrough videos with the goal of quickly teaching a novice computer learner to play the game?
Can an expert computer learner provide meaningful annotations to a novice computer learner, or real-time feedback on performance to increase the rate at which rules are learned?
Can an expert computer learner provide useful feedback to a novice human learner, to help them improve areas they are having trouble with or provide suggestions for a puzzle they can't solve?
Can we learn other digital tasks such as removing red-eye in photoshop or arranging objects in PowerPoint?

Rule and value function learning

Within each genre, what are the common types of rules, and can we use this knowledge to play new games better?
What parts of human experience are critical for rule discovery? Which can be learned by experimenting with games?
How much faster can we learn the rules to 10x10 checkers if we already know the rules to 8x8 checkers?
How well can we play if we only know some of the rules to a game? How much does this depend on genre?
If each human play-through is annotated with a user ID, can we learn different value functions for each player? Can we determine which players are more skilled?
Given multiple value functions learned from multiple users, can we use both unskilled and moderately skilled players to extrapolate what constitutes skilled gameplay?

Natural language processing

Can we write a useable rulebook for a game or make a map of the game world?
Given a learned model of the game and the game's Wikipedia page, can we connect entities in our game to objects described in the rules and figure out the names humans use?
Can we use a game's Wikipedia page to make our game learner more efficient?

Conclusion

At present general game learning remains a fledgling field. In the beginning it is unlikely that learners will be effective beyond somewhat constrained 2D environments that can be approximately decomposed into entities such as sprites and text. After successful 2D learners exist it might be possible to try using 3D computer vision techniques to categorize and isolate the entities in the game. An alternative route is to extract some meaningful representation by leveraging the segmentation used internally by the game, as was done for example in a StarCraft 2 AI by intercepting rendering commands as they were sent to the graphics card for processing.

We have used several recurring examples such as Chess and Super Mario Brothers when describing various components of general game learning. This is not because the goal of GGL is to focus on these two types of games: anything that falls under the human notion of a game is something worth trying to learn. Below we give a much broader survey of games (which is by no means exhaustive), each of which likely presents several unique challenges and interesting insights into the learning problem.