 |
| Regular structures discovered by our algorithm involve combinations of rotation,
translation, and scaling of the repetitive elements.
|
| |
 |
| Schematic illustration of regular structures. The helix and spiral are generated by transformations that combine rotation with translation
and scaling, respectively. The images on the right show the three types of commutative 2-parameter groups: rotation and translation
along the rotation axis, two independent translations, rotation and scaling with center of scaling on the rotation axis.
|
| |
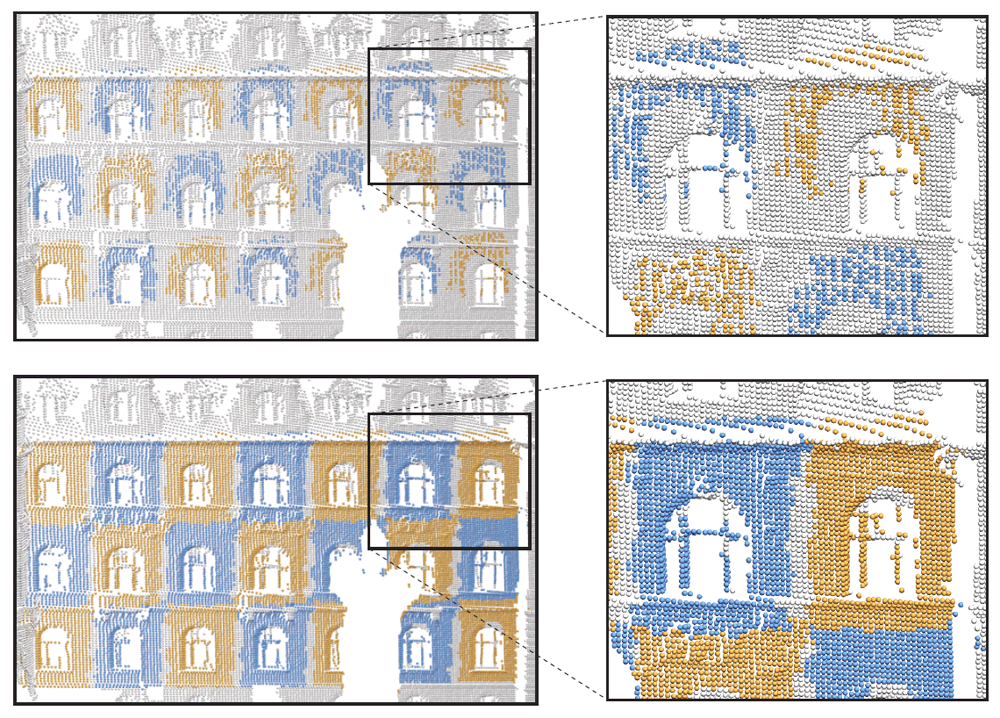
| Simultaneous Registration. The colored points show
the sample points that are closest to the bottom left element transformed
using the estimated group transformations. Aggregation
without registration leads to successively stronger misalignments
(top row). Our coupled optimization with simultaneous registration
significantly improves the accuracy of the generating transformations
and allows extracting larger elements (bottom row). |
|
 |
|
| |
 |
|
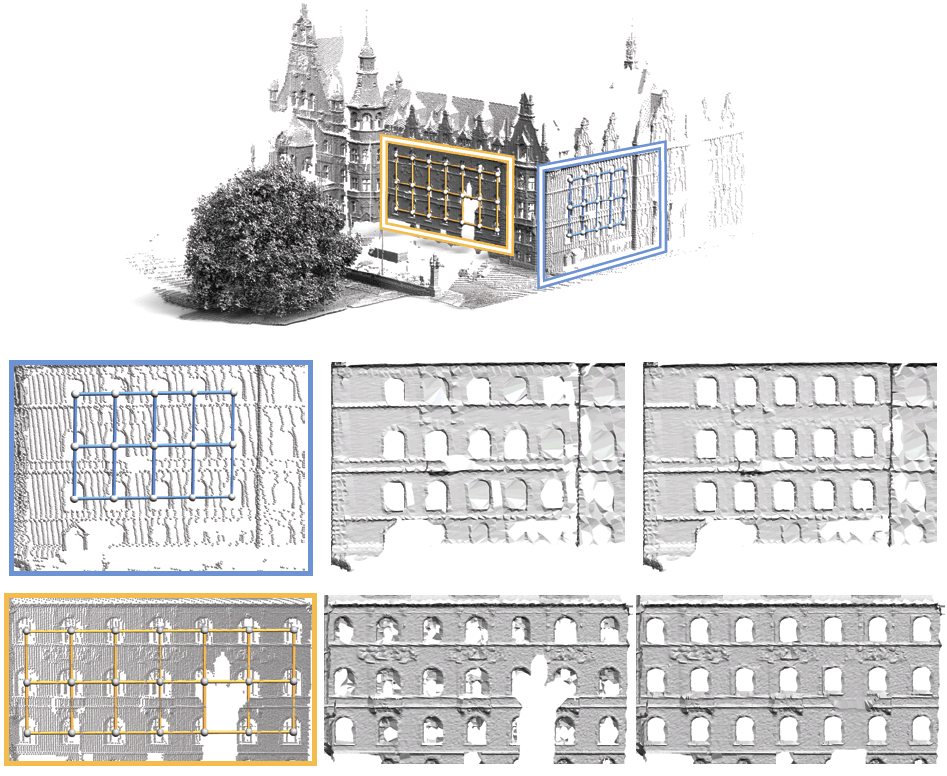
Structure detection and model repair on a complex outdoor
scan. Our algorithm fully automatically discovers two translational
grids within the acquired point cloud. Standard surface
reconstruction yields an incomplete and inconsistent triangulation
shown in the middle. The models on the right have been created by
augmenting the point set using replicated samples from the representative
elements prior to reconstruction. |
|
| |
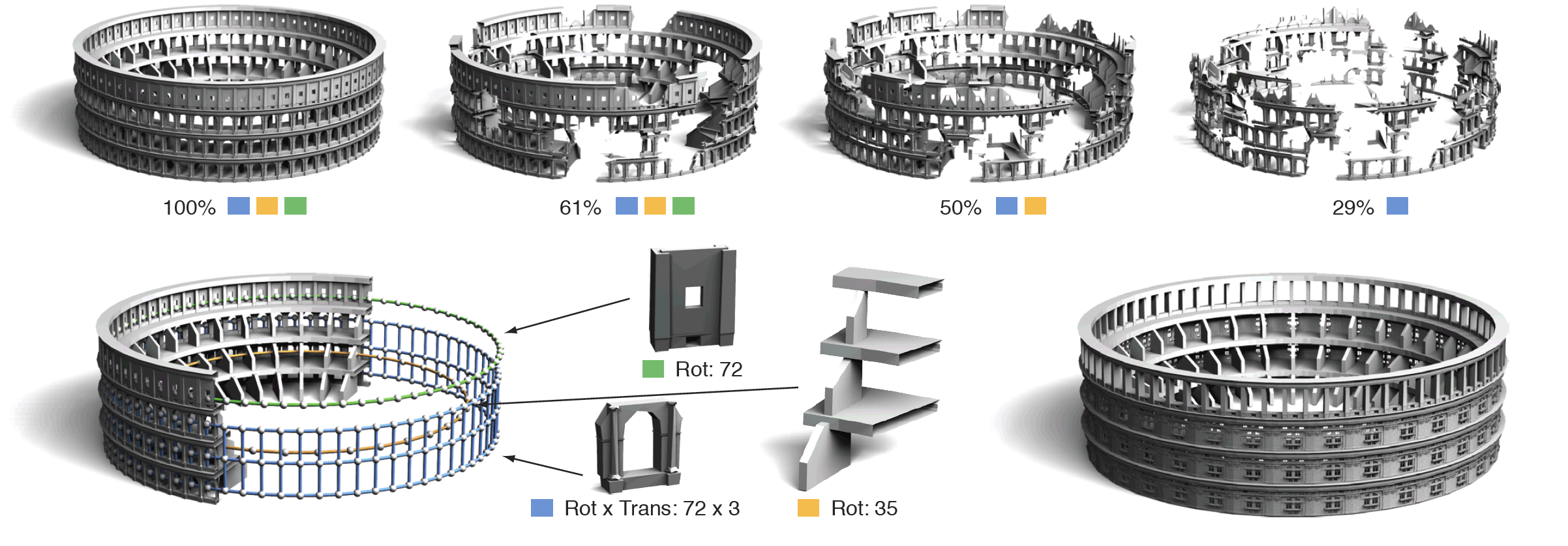 |
| Structure discovery and procedural design on a 3D model of an amphitheater. The top row indicates which of the three regular
structures can be reconstructed in their entirety when successively removing geometry. The density plots show a section of the distribution of
transformations of the structure depicted in blue. The recovered structures are used to procedurally design a new model in the bottom right.
|
| |
 |
| Our method detects multiple 1- and 2-parameter structures. The blue regions denote the representative elements. All structures
where detected with 30k samples distributed uniformly across the model, except for the balustrade, for which the rate was increased to 100k.
|
| |
 |
| Model repair and geometry synthesis for a scan of a chambered nautilus shell. From left to right: photograph of original model,
input data consisting of 72 registered laser scans, repaired model with additional synthesized elements indicated in orange.
|
| |
Bibtex:
@article{pmwpg_structure_sig_08,
AUTHOR = "M. Pauly and N. J. Mitra and J. Wallner and H. Pottmann and L. Guibas",
TITLE = "Discovering Structural Regularity in {3D} Geometry",
JOURNAL = "ACM Transactions on Graphics",
VOLUME = "27",
NUMBER = "3",
PAGES = "\#43, 1-11",
YEAR = "2008",
}






