, ``Topological Map''.
In this chapter we introduce the planar map which is an
embedding of a topological map into the plane.
It is derived
from the topological map class with additional geometric considerations
and functionalities (e.g., point location). In this section we briefly review
the geometric concepts added in the planar map, the combinatorial concepts were
reviewed in Chapter , ``Topological Map''.
Curve: We will use the term curve to describe the image of a continuous mapping into the plane of any one of the following: the closed unit interval (arc), the open unit interval (unbounded curve), or the unit circle (closed curve). In all cases a curve is non self-intersecting.
-Monotone curve: We use a convention that a curve is -monotone if either intersects any vertical line in at most one point, or is a vertical segment.
Planar subdivision (planar map): A planar subdivision (or planar map) is an embedding of a planar topological map into the plane, such that each edge of is embedded as a bounded -monotone curve and each vertex is embedded as a planar point. In this embedding no edge intersects another edge's interior.
A face of the subdivision is a maximal connected region of the plane that does not contain any vertex or edge. We consider a face to be open, and its boundary is formed by vertices and halfedges of the subdivision. The halfedges are oriented around a face so that the face they bound is to their left. This means that halfedges on the outer boundary of a face are traversed in counterclockwise order, and halfedges on the inner boundaries (holes) of a face are traversed in clockwise order. Edges around a vertex are also traversed in clockwise order.
We have derived three concrete classes for point location strategies which are
presented at Section - .
#include <CGAL/Pm_default_point_location.h>
|
| |
|
constructs the point location object. If preprocess is true then
preprocessing is done to guarantee a deterministic worst case query time of
log. However, the preprocessing step can slow down considerably
the building time of the structure.
| |
#include <CGAL/Pm_naive_point_location.h>
The Pm_walk_along_line_point_location<Planar_map> class implements a walk-along-a-line algorithm which improves the naive one. Unlike the naive algorithm which goes over all the edges of the planar map, the walk algorithm starts with the unbounded face and ``walks'' along the zone of the vertical ray emanating from the query point. This reduces the number of halfedges that are traversed in a query. Like the naive strategy, the walk strategy does not use an additional structure. The updating operations are empty and therefore modifying operations such as split_edge and merge_edge take constant time.
#include <CGAL/Pm_walk_along_line_point_location.h>
Another trade-off depends on the need for point location queries compared to the need for other functions. If the users do not need point location queries, but do need other modifying functions (e.g., remove_edge, split_edge and merge_edge) then using the naive or walk strategies is preferable. Note that using the insert function invokes the point location query, therefore when using the naive or walk strategies it is recommended to use the specialized insertion functions : insert_in_face_interior, insert_from_vertex and insert_at_vertices. For example, when using the planar map to represent polygons (e.g., when computing boolean operations on polygons) it might be preferable to use the walk strategy with the specialized insertion functions.
Another trade-off is between the two modes of the default strategy. If preprocessing is not used, the building of the structure is faster. However, for some input sequences the structure might be unbalanced and therefore queries can take longer.
The planar map class is parameterized with the interface classes Dcel and Traits . The Dcel class is a container class that defines the underlying combinatorial data structure (halfedge data structure) used by the planar map. The Traits class defines the abstract interface between planar maps and the geometric primitives they use.
The requirements for a Dcel class of a planar map are identical to those required for a Dcel class of a topological map. In addition the Vertex and Halfedge classes for the planar map are required to have geometric functionality. The requirements are stated below.
The Pm_dcel<V,H,F> is a model of the Dcel concept defined above. Its template parameters are the vertex, halfedge and face classes which conform to the requirements given above.
#include <CGAL/Pm_default_dcel.h>
#include <CGAL/Pm_default_dcel.h>
#include <CGAL/Pm_default_dcel.h>
The planar map class is parameterized with the interface class Traits which defines the abstract interface between planar maps and the primitives they use. The following requirement catalog lists the primitives, i.e., types, member functions etc., that must be defined for a Traits class that can be used to parameterize planar maps.
We supply a default traits class for exact arithmetic - Pm_segment_exact_traits<R> where R is the kernel representation type (Homogeneous or Cartesian). There is also a class for finite precision arithmetic - Pm_segment_epsilon_traits<R>, which is not recommended unless it is known that robustness issues will not arise. Both traits handle finite line segments in the plane and use the CGAL kernel (Point is of type Point_2<R> and X_curve is of type Segment_2<R>). We also supply a traits class that uses LEDA's rational kernel and makes use of its efficient predicates.
Figure: The map generated by the example program
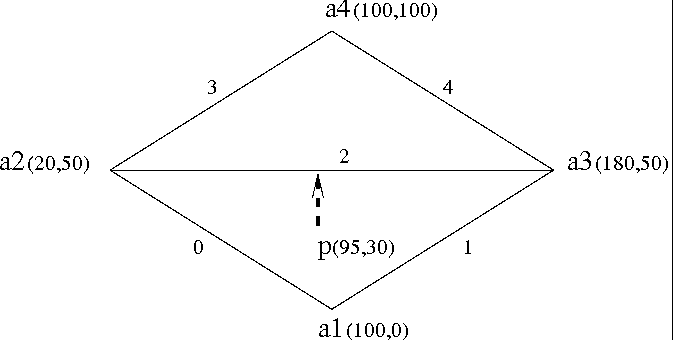
The following program creates a planar map from five curves (see
figure ). It uses the floating-point
arithmetic interface class
(Pm_segment_epsilon_traits<R>). The first part of the
code initializes five segments. The next part inserts them to the map
and checks the validity of the map. In the last part, a vertical ray
shooting is performed from the point .
#include <CGAL/Cartesian.h>
#include <CGAL/Pm_segment_epsilon_traits.h>
#include <CGAL/Pm_default_dcel.h>
#include <CGAL/Planar_map_2.h>
typedef double number_type;
typedef Cartesian<number_type> coord_t;
typedef Pm_segment_epsilon_traits<coord_t> pmtraits;
typedef typename pmtraits::Point point;
typedef typename pmtraits::X_curve curve;
typedef Pm_default_dcel<pmtraits> pmdcel;
int main()
{
// creating an instance of Planar_map_2<pmdcel,pmtraits>
Planar_map_2<pmdcel,pmtraits> pm;
curve cv[5];
int i;
point a1(100, 0), a2(20, 50), a3(180, 50), a4(100, 100);
// those curves are about to be inserted to pm
cv[0] = curve(a1, a2);
cv[1] = curve(a1, a3);
cv[2] = curve(a2, a3);
cv[3] = curve(a2, a4);
cv[4] = curve(a3, a4);
cout << "the curves of the map :" << endl;
for (i = 0; i < 5; i++)
cout << cv[i] << endl;
cout << endl;
// insert the five curves to the map
cout << "inserting the curves to the map..." << endl;
for (i = 0; i < 5; i++)
{
cout << "inserting curve" << i << endl;
pm.insert(cv[i]);
}
// check the validity of the map
cout << "check map validity... ";
if (pm.is_valid())
cout << "map valid!" << endl;
else
cout << "map invalid!" << endl;
cout << endl;
// vertical ray shooting upward from p
point p(95, 30);
typename Planar_map_2<pmdcel,pmtraits>::Halfedge_handle e;
typename Planar_map_2<pmdcel,pmtraits>::Locate_type lt;
cout << endl << "upward vertical ray shooting from " << p << endl;
e=pm.vertical_ray_shoot(p, lt, true);
if (lt != Planar_map_2<pmdcel,pmtraits>::UNBOUNDED_FACE) {
cout << "returned the curve :" << e->curve() << endl;
}
return 0;
}
The output of this program is
the curves of the map : 100 0 20 50 100 0 180 50 20 50 180 50 20 50 100 100 180 50 100 100 inserting the curves to the map... inserting curve0 inserting curve1 inserting curve2 inserting curve3 inserting curve4 check map validity... map valid! upward vertical ray shooting from 95 30 returned the curve : 20 50 180 50