Triangulation in 3D

Introduction

Definition

The basic 3D-triangulation class of CGAL is primarily designed to represent the triangulations of a set of points $$A in $$ ³. It can be viewed as a partition of the convex hull of $$A into tetrahedra whose vertices are the points of $$A. Together with the unbounded cell having the convex hull boundary as its frontier, the triangulation forms a partition of $$ ³.

In order to deal only with tetrahedra, which is convenient for many applications, the unbounded cell can be subdivided into tetrahedra by considering that each convex hull facet is incident to an infinite cell having as fourth vertex an auxiliary vertex called the infinite vertex. In that way, each facet is incident to exactly two cells and special cases at the boundary of the convex hull are simple to deal with.

The class Triangulation_3<Traits,Tds> of CGAL implements this point of view and therefore considers the triangulation of the set of points as a set of finite and infinite tetrahedra. Notice that the infinite vertex has no significant coordinates and that no geometric predicate can be applied on it.

A triangulation is a collection of vertices and cells that are linked together through incidence and adjacency relations. Each cell gives access to its four incident vertices and to its four adjacent cells. Each vertex gives access to one of its incident cells.

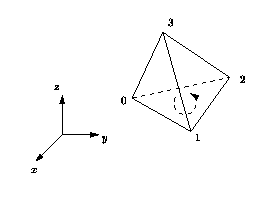
The four vertices of a cell are indexed with 0, 1, 2 and 3 in positive orientation, the positive orientation being defined by the orientation of the underlying Euclidean space $$ ³. The neighbors of a cell are also indexed with 0, 1, 2, 3 in such a way that the neighbor indexed by $$i is opposite to the vertex with the same index. See Figure .

Figure:  Orientation of a cell (3-dimensional case)

As in the underlying combinatorial triangulation (see Chapter ), edges ($$1-faces) and facets ($$2-faces) are not explicitly represented: a facet is given by a cell and an index (the facet i of a cell c is the facet of c that is opposite to the vertex with index i) and an edge is given by a cell and two indices (the edge (i,j) of a cell c is the edge whose endpoints are the vertices of c with indices i and j). See Figure .

Degenerate Dimensions

The class Triangulation_3<Traits,Tds> can also deal with triangulations whose dimension is less than 3. A triangulation of a set of points in $$ ^d covers the whole space $$ ^d and consists of cells having $$d+1 vertices: some of them are infinite, they are obtained by linking the additional infinite vertex to each facet of the convex hull of the points.

• dimension 2: when a triangulation only contains coplanar points (which is the case when there are only three points), it consists of triangular faces.
• dimension 1: the triangulation contains only collinear points (which is the case when there are only two points), it consists of edges.
• dimension 0: the triangulation contains only one finite point.
• dimension -1: this is a convention to handle the case when the only vertex of the triangulation is the infinite one.

The same cell class is used in all cases: triangular faces in 2D can be considered as degenerate cells, having only three vertices (resp. neighbors) numbered $$(0,1,2), and one $$NULL vertex (resp. neighbor); edges in 1D have only two vertices (resp. neighbors) numbered $$0 and $$1.

The implicit representation of facets (resp. edges) still holds for degenerate dimensions (i.e.dimensions $$<3) : in dimension 2, each cell has only one facet of index 3, and 3 edges $$(0,1), $$(1,2) and $$(2,0); in dimension 1, each cell has one edge $$(0,1).

Validity

A triangulation of $$ ³ is said to be locally valid iff

(a)-(b) Its underlying combinatorial graph, the triangulation data structure, is locally valid (see Section  of Chapter )
(c) Any cell has its vertices ordered according to positive orientation. See Figure .

When the triangulation is degenerated into a triangulation of dimension 2, the geometric validity reduces to:

(c-2D) For any two adjacent triangles $$(u,v,w₁) and $$(u,v,w₂) with common edge $$(u,v), $$w₁ and $$w₂ lie on opposite sides of $$(u,v) in the plane.

When all the points are collinear, this condition becomes:

(c-1D) For any two adjacent edges $$(u,v) and $$(v,w), $$u and $$w lie on opposite sides of the common vertex $$v on the line.

The is_valid() method provided by CGAL checks the local validity of a given triangulation. This does not always ensure global validity [MNS$$⁺96, DLanRT98] but it is sufficient for practical cases.

Software Design

The class Triangulation_3<Traits,Tds> is designed to be used as a layer upon a 3D-triangulation data structure as presented in Section  of Chapter . It provides high level geometric operations such as location of a point in the triangulation and insertion of a point, and is responsible for the geometric validity. This class is parameterized by two classes:

• the geometric traits class, where the user can specify the type of points to use as well as the elementary operations on them (predicates,...). The concept of such a class is described in Section  and a model is provided by CGAL (see Section ).
• the triangulation data structure class of the middle level, described in Chapter .

Delaunay triangulations as well as hierarchical Delaunay triangulations [Dev98] are also implemented in the package: Delaunay_triangulation_3<Traits,Tds> inherits from Triangulation_3<Traits,Tds> and Delaunay_hierarchic_triangulation_3<Traits,Tds> inherits from Delaunay_triangulation_3<Traits,Tds>. (Hierarchical Delaunay triangulations are not yet implemented.)

Triangulation_3<Traits,Tds> derives from Triangulation_utils_3<Traits,Tds>, which defines a set of tools working on the indices of vertices in cells (see Section ).

Examples

#include <CGAL/basic.h>

#include <iostream>

#include <list>
#include <vector>

#include <CGAL/Cartesian.h>

#include <CGAL/Triangulation_cell_base_3.h>
#include <CGAL/Triangulation_vertex_base_3.h>
#include <CGAL/Triangulation_data_structure_3.h>
#include <CGAL/Triangulation_geom_traits_3.h>
#include <CGAL/Triangulation_3.h>

typedef CGAL::Cartesian<double>  Rep;

typedef CGAL::Triangulation_geom_traits_3<Rep> Gt;
typedef CGAL::Triangulation_vertex_base_3<Gt> Vb;
typedef CGAL::Triangulation_cell_base_3<Gt>  Cb;

typedef CGAL::Triangulation_data_structure_3<Vb,Cb> TDS;
typedef CGAL::Triangulation_3<Gt,TDS> Triangulation;

typedef typename Triangulation::Cell_handle Cell_handle;
typedef typename Triangulation::Vertex_handle Vertex_handle;
typedef typename Triangulation::Locate_type Locate_type;

typedef Gt::Point Point;

int main(int argc, char* argv[])
{

  Triangulation T;

  // insertion from a list :
  std::list<Point> L;
  L.push_front(Point(0,0,0));
  L.push_front(Point(1,0,0));
  L.push_front(Point(0,1,0));

  int n = T.insert(L.begin(), L.end());

  // insertion from a vector :
  std::vector<Point> V(3);
  V[0] = Point(0,0,1);
  V[1] = Point(1,1,1);
  V[2] = Point(2,2,2);

  n = n + T.insert(V.begin(), V.end());

  // 6 points have been inserted :
  assert( n == 6 );

  // checking validity of T :
  assert( T.is_valid(false) );

  Locate_type lt;
  int li, lj;
  Point p(0,0,0);
  Cell_handle c = T.locate(p, lt, li, lj);
  // p is the vertex of c of index li :
  assert( lt == Triangulation::VERTEX );
  assert(  c->vertex(li)->point() == p );

  Vertex_handle v = c->vertex( (li+1)&3 );
  // v is another vertex of c
  Cell_handle nc = c->neighbor(li);
  // nc = neighbor of c opposite to the vertex associated with p
  // nc must have vertex v :
  int nli;
  assert( nc->has_vertex( v, nli ) );
  // nli is the index of v in nc

  std::ofstream oFileT("output",ios::out);
  // writing file output; 
  oFileT << T; 

  return 0;
}

A Class of Tools

• Class declaration of Triangulation_utils_3.

Basic Triangulation

Definition

• Class declaration of Triangulation_3<Traits,Tds>.

The Vertex of a Triangulation

• Class declaration of Triangulation_vertex_3<Traits,Tds>.

The Cell of a Triangulation

• Class declaration of Triangulation_cell_3<Traits,Tds>.

Delaunay Triangulation

• Class declaration of Delaunay_triangulation_3<Traits,Tds>.

Hierarchic Delaunay Triangulation

(See [Dev98].)

• Class declaration of Delaunay_hierarchic_triangulation_3<Traits,Tds>.

Regular Triangulation

• Class declaration of Regular_triangulation_3<Traits,Tds>.

The Geometric Traits

The first template parameter of the triangulation class Triangulation_3<Traits,Tds> of CGAL is the geometric traits class.

The first subsection of this section describes the requirements that a geometric traits class must fulfill. The second subsection presents a predefined geometric traits class available in CGAL.

Concept for the Geometric Traits Class

• Class declaration of Triangulation_Traits_3.

Model for the traits class

• Class declaration of Triangulation_geom_traits_3<R>.

Model for the traits class of a regular triangulation

• Class declaration of Regular_triangulation_euclidean_traits_3<R,Weight>.

Weighted point

Concept for a weighted point

The weighted point class must fulfill the following requirements:

Types

Creation

wp ( Point p=Point(), Weight w = Weight(0));

Access Functions

Model of weighted point

• Class declaration of Weighted_point<Point,Weight>.

The Triangulation Data Structure Parameter

The second template parameter of the basic triangulation class Triangulation_3<Traits,Tds> is a triangulation data structure class. This class can be seen as a container for the cells and vertices maintaining incidence and adjacency relations.

The concept for the triangulation data structure is described in Section  of Chapter . Its optional arguments related to geometry are compulsory for this use as a template parameter of Triangulation_3<Traits,Tds>. A model of this triangulation data structure is Triangulation_data_structure_3 presented in Section .