Tamara Munzner, Stanford University
![]()
We present the H3 layout technique for drawing large directed graphs as node-link diagrams in 3D hyperbolic space. We can lay out much larger structures than can be handled using traditional techniques for drawing general graphs because we assume a hierarchical nature of the data. We impose a hierarchy on the graph by using domain-specific knowledge to find an appropriate spanning tree. Links which are not part of the spanning tree do not influence the layout but can be selectively drawn by user request.
The volume of hyperbolic 3-space increases exponentially, as opposed to the familiar geometric increase of euclidean 3-space. We exploit this exponential amount of room by computing the layout according to the hyperbolic metric. We optimize the cone tree layout algorithm for 3D hyperbolic space by placing children on a hemisphere around the cone mouth instead of on its perimeter. Hyperbolic navigation affords a Focus+Context view of the structure with minimal visual clutter. We have successfully laid out hierarchies of over 20,000 nodes. Our implementation accommodates navigation through graphs too large to be rendered interactively by allowing the user to explicitly prune or expand subtrees.
Directed graphs are an appealing target for visualization because of their pervasive presence in information systems. Many of the structures which permeate computer science can be represented as node-link graphs. The examples shown in this paper include function call graphs, the directory structure of Unix file systems, and the link structure of the World Wide Web.
Computing a layout for a general graph is a difficult problem, while tree layout is much more tractable. Many directed graphs which appear to be unstructured meshes when considered as abstract graphs do in fact have a hierarchical structure when we exploit domain-specific knowledge. We will call such graphs hierarchical graphs in this paper. We use domain knowledge when available to construct an appropriate spanning tree for a hierarchical graph. Our placement decisions are based only on the spanning tree, but we support selective drawing of nontree links to show the general graph structure. We can handle nonhierarchical graphs by constructing a spanning tree based only on graph theoretic criteria such as distance from the root node, but the resulting visualization may not provide much insight into the graph structure. Our layout does works very well with trees, which we include as a subset of hierarchical graphs.
The Web is an interesting problem domain because while it is highly interconnected, the designer of a Web site usually has a clear notion of hierarchy within the site. Visualizing the Web has become a recurring theme in the information visualization literature. Many researchers have striven to ameliorate the ``lost in hyperspace'' problem which plagues surfers who use traditional browsers with one-dimensional history lists. Providing a visual context for the display of search results has been another motivation. Webmasters and content creators are interested in seeing both the static structure of their site and dynamic traffic patterns through the site structure. Web visualization will be a driving example throughout this paper.
The classic problem with tree layout in euclidean space is that the number of nodes grows exponentially, but the circumference of a circle or the area of a sphere grows only polynomially. To avoid collisions we must allocate less room to nodes which occur deeper in the tree. When we zoom back to see an overview of the entire tree, the only nodes which we can see in detail are those surrounding the root node. If we want to examine nodes deeper in the tree we must zoom in so far that we lose all sense of surrounding context.
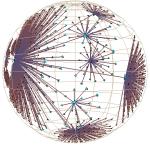
In hyperbolic space, circumference and area increase exponentially instead of geometrically. There is enough room to allocate the same amount of space to every node, no matter how deep in the tree. Although hyperbolic space is infinite, we can project it into a finite volume of euclidean space for a Focus+Context view. When we lay out and move trees using hyperbolic distances, we can see details in a neighborhood around a node of current interest while retaining an overview of the larger structure. Although distant features are quite distorted, we see far more surrounding context than we ever could in a euclidean representation. This feature is particularly important when we want to show the destinations of nontree links, which may be quite far away from the originating node. We see an example of a hierarchical graph drawn in 3D hyperbolic space in Figure 1.
The structure of the rest of the paper is as follows: in Section 2 we cover related work. We discuss our layout algorithm in Section 3, and relevant topics in hyperbolic geometry in Section 4. We summarize implementation issues in Section 5 and then analyze our results in Section 6. Future work is covered in Section 7, and we conclude in Section 8. Appendix A contains a derivation of the hyperbolic layout parameters.
A good overview of the 3D information visualization literature can be found in Peter Young's survey paper [You96]. The most relevant areas related to the H3 layout technique are graph drawing and Focus+Context techniques.
The field of graph drawing has developed some effective solutions for handling relatively small graphs. Traditional graph layout techniques which work on general graphs are extremely effective for dozens of nodes, can sometimes handle hundreds, and generally break down completely for thousands of nodes. One relatively recent paper [FLM94] characterized graphs as tiny, small, medium, large, and huge respectively as having node counts of 16, 32, 64, 128, and more than 128. These numbers may seem surprisingly small to members of the visualization community, and serve to illustrate the difficulty of finding an aesthetic layout of a general graph. The extensive annotated bibliography of Battista et al [BETT94] provides a good overview of the state of the field in 1994.
Several systems devoted to Web visualization draw on the techniques of
graph drawing and use abstract node-link diagrams in two dimensions.
The early Webmap system constructs a spanning tree of the documents
visited in a browsing session, drawing both the spanning tree and
non-tree links in two dimensions [Doe94]. The WebViz system
for Web log analysis from Georgia Tech uses the expedient but crude
approach of laying out the nodes randomly
[PB94] ![]() . The MosaicG system, also from Georgia
Tech, incorporates a 2D history browser into Mosaic itself
[AS95]. Its features include two levels levels of detail
(drawing nodes as document thumbnails or as simple boxes), subtree
collapsing and expansion, and a more sophisticated ``tidy tree''
layout mechanism.
. The MosaicG system, also from Georgia
Tech, incorporates a 2D history browser into Mosaic itself
[AS95]. Its features include two levels levels of detail
(drawing nodes as document thumbnails or as simple boxes), subtree
collapsing and expansion, and a more sophisticated ``tidy tree''
layout mechanism.
The 2 ![]() dimensional landscape of the SGI fsn
filesystem viewer [TS] employed a very concrete metaphor
where documents are represented as building-like structures which rise
above a ground plane. The Harmony Information Landscape
[APW96] extended this metaphor to more fully exploit 3D space
by showing hyperlink relationships between Web or Hyper-G documents
superimposed above and below the decorated plane.
dimensional landscape of the SGI fsn
filesystem viewer [TS] employed a very concrete metaphor
where documents are represented as building-like structures which rise
above a ground plane. The Harmony Information Landscape
[APW96] extended this metaphor to more fully exploit 3D space
by showing hyperlink relationships between Web or Hyper-G documents
superimposed above and below the decorated plane.
Iterative force-directed placement systems model nodes and links as a mass-spring system, where nodes repulse each other but links exert an attractive force. The Gem3D system for general graphs [BF95] and the Hyper/Narcissus system for Web visualization [HDWB95] both use force-directed layout. While these iterative systems do well with relatively small graphs they have difficulty converging when the number of nodes scales from hundreds to thousands. The Narcissus constructs a graph based on the semantic content of documents. In contrast, we focus on the problem of graph layout and navigation for a given input graph rather than the problem of constructing that input graph. We do make use of domain-specific semantics, but only to to determine a spanning tree through an existing graph rather than to construct that graph from a set of nodes.
Although the H3 layout technique handles graphs, our methodology has more in common with tree drawing methods than with drawing general graphs. The cone tree system from Xerox PARC [RMC91] introduced one of the most influential techniques in 3D tree drawing. Carrière and Kazman [CK95] proposed a more sophisticated bottom-up layout technique to minimize the chances that cone would have overlapping territories. The webviz system extended cone trees from euclidean to hyperbolic space [MB95].
Methods of introducing deliberate distortion in order to show a large amount of contextual information in a given amount of screen area are collectively known as Focus+Context views. Some papers, including the original cone tree paper [RMC91], advocate using 3D euclidean perspective to achieve this goal. A more aggressive approach is to view a graph through a fisheye lens [SB94, KRB94], or drawn on a stretchable rubber sheet [SSTR93, SCCF95]. Taxonomies by Noik [Noi94] and Leung and Apperley [LA94] present a useful analysis of Focus+Context techniques, which we will not duplicate here. Noik in particular discusses Focus+Context techniques as they relate to graph drawing. The H3 method is more similar to single-focus fisheye techniques than to the multiple-focus rubber sheet methods. In Section 4 we discuss in depth the advantages of hyperbolic layout over fisheye lens techniques.
The fractal tree work of Koike and Yoshimara [KY93] is similar in spirit to hyperbolic approaches. Both tame the exponential explosion of tree nodes by drawing trees in a mathematical space with nonstandard properties - dimension or distance, respectively. While the fractal tree work was an intriguing beginning and included a 3D view, their system did not tackle the 3D layout problems of ensuring that subtrees do not overlap in space.
The first hyperbolic visualization system described in the information visualization literature was the 2D hyperbolic tree browser from Xerox PARC [LR94]. The webviz hyperbolic browser from the Geometry Center [MB95] handled general graphs in 3D. The webviz layout algorithm did not exploit 3D hyperbolic space to its full potential: the amount of displayed information compared to the amount of white space was quite sparse. Moreover, the webviz system drew all links in the graph at all times, so highly connected graphs were quite cluttered.
The H3 layout scheme consists of two parts: we must first find an appropriate spanning tree from an input graph. We then determine a position in space for each element of that tree in space. Non-tree links do not affect the layout decision, and are only drawn on request. The spanning tree links are always drawn. We lay out the entire structure and then change the focus by hyperbolic navigation. This section contains a discussion of our layout approach and Appendix A contains a detailed derivation of the hyperbolic layout parameters.
The choice of spanning tree is fundamental in shaping the visualization of the graph. While we can construct a spanning tree based only on the link structure of the graph, domain-specific knowledge will usually help impose a tree structure that matches the user's expectations. Our current system uses domain knowledge to disambiguate, not override, the link structure of the graph. We discuss examples in three domains:
![]() Directory structure of a Unix file system
Directory structure of a Unix file system
Leaf nodes represent files and interior nodes represent directories. File systems tend to be nearly trees: nontree edges represent symbolic links, which are relatively rare. The full path name of a file mirrors the link structure of the input graph, so domain knowledge is not important in this case.
![]() Hyperlink structure of the Web
Hyperlink structure of the Web
Nodes represent Web documents and the links represent hyperlinks between those documents. The link structure is usually quite different from the directory structure in which those documents are kept on the file system. When we simply use the link traversal of the graph to determine parentage, the resulting tree is generally not very close to the authorial intent of the Web designer. For instance, the top-level document at a site may contain a link to a table of contents page, which in turn contains a link to every other document at that site. According to the link structure of the graph, that table of contents document would be the main parent of most of those nodes. The URL encodes the place of a Web document in the Unix directory structure. We use this directory information to make a decision to decide which of the hyperlinks to a document should be used as its main parent in the tree. Note that this use of directory information to resolve parentage within the context of the link structure is not the same as simply laying out a graph of the file system. We also use the Web domain knowledge that file names ending in i.e. index.html should be the parent of other files which share a directory.
One advantage of this heuristic is that it makes a common breakdown very visible to the user. Orphan documents are those whose directory-structure parents are not listed as possible parents in the link traversal of the graph. Orphans are often the result of inadvertently broken links. Our heuristic places these nodes near the top of the tree rather than among their directory-structure peers, so they stand out.
![]() Function call graphs
Function call graphs
Nodes represent functions and the links represent a call from one function to another. Our example is a call graph for a FORTRAN scientific computing benchmark. Although we cannot simply glean hierarchical information from function names, we can use a combination of compiler analysis and dynamic profile information to determine a reasonable spanning tree. The calling procedure which is responsible for the majority of the child's execution time is chosen as the main parent.
In traditional cone trees nodes are laid out on a circle: the circumference of the disc at the bottom of the cone. In the H3 algorithm we lay them out on a hemisphere: a spherical cap which covers the cone mouth. Figure 2a compares the two layouts for the same data set, a single generation of children. We use hemispheres instead of full spheres since we only have an exponential amount of room when in the direction radially outward from the origin.
The algorithm requires two passes: a bottom-up pass to determine the radius of the hemispheres, and a top-down pass to lay out the child nodes on the surface of their parental hemisphere. We cannot combine these steps because we must know the radius of the parent hemisphere before we can compute the final position of each child hemisphere.
![]() Bottom-up pass:
Bottom-up pass:
We know the radius of each of the child hemispheres and must determine how large of a hemisphere to allocate for the parent hemisphere. Ideally we would consider the area of the spherical caps covered by child hemispheres, and sum them to get the necessary area for the parent hemisphere. However, the computation of the area of spherical cap requires knowledge about the radius of the parental hemisphere, which is just what we are trying to find. We instead use the area of the disc at the bottom of the child hemisphere as an acceptable approximation. This approximation is quite close when the child hemisphere subtends a small angle; that is, when a parent has many child nodes. The approximation breaks down when the number of children is very small, but this situation is easy to handle with special cases. Leaf nodes are drawn as tetrahedra of a fixed hyperbolic size in this implementation, so we know the value of the radius in the base case.
![]() Top-down pass:
Top-down pass:
We know at every level the radius of the parent hemisphere but must decide how to lay out the children on its surface. This decision is an instance of the sphere-packing problem, which has been extensively explored by mathematicians. Our particular instance is that of packing 1-spheres (i.e. circles) on the surface of a 2-sphere (i.e. an ordinary sphere) [CS88]. A related problem is that of distributing points evenly on a sphere [SK97].
The particular requirements of our situation are somewhat different than the usual cases addressed in the literature. Our circles are of variable size, and we are interested in a hemisphere as opposed to a sphere. More importantly, our solution must be fast and repeatable. Our solution cannot involve randomness: given the same input, we must generate the same canonical output. We care far more about speed than precision. An approximate layout is fine for our purposes, while a perfect but slow iterative solution would be inappropriate.
Our solution is to lay out the discs in concentric bands centered along the pole normal to the sphere at infinity. We sort the child discs by the size of their hemispheres. This number, which is recursively calculated in the first bottom-up pass, depends on the total number of their descendants, not just their first-generation children. The ones which require the most area (i.e. the ones with the most progeny) are closest to this pole. Figure 3 shows a view of a parent hemisphere from the side, drawing only the footprints of the child hemispheres. The equatorial (bottom-most) band is usually only partially complete.
One advantageous result of our choice to order by number of progeny is that the complex part of structures is always easy to locate. An investigation of the tradeoffs of other ordering criteria would be worth undertaking.
Figure 3: Disks at the bottom of child hemispheres are laid out in bands on the parent in sorted order according to the number of their descendants, with the most prolific at the pole.
Even if our circle packing were optimal, the area of the hemisphere required to accommodate the circles would be greater than the sum of the spherical caps subtended by those circles, since we do not take into account the uncovered gaps between the circles. Moreover, our banding scheme, while relatively easy to implement, is definitely a suboptimal circle packing. We waste the leftover space in the equatorial band, which in the worst case contains only a single disc. If we did not sort the child discs by size the discrepancy would be even worse. Finally, the above-mentioned difference between the area of a disc and the area of the spherical cap contributes to the total discrepancy
We chose to deal with this discrepancy by increasing the radius of the parental hemisphere by a factor proportional to the originally computed radius. A possible alternative would be to use the computed radius as the base for an iterative solution. While this iteration would probably converge quickly, our empirically derived factor works well in practice.
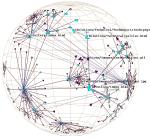
Figure 4 is a sequence showing motion through several generations of a tree representing a Unix file system of 2000 nodes.
Our layout is computed using hyperbolic distances instead of the familiar euclidean distance measure. We use the hyperbolic metric in order to take advantage of the surprising property that hyperbolic space has more room than our familiar euclidean space. Two parallel lines are always the same distance apart in euclidean space. However, in hyperbolic space, parallel lines are not equidistant. We can construct two hyperbolic straight lines which do not intersect yet are separated by increasing distance as we move away from the origin. Figure 5 contains a sketch of both sets of lines. Further explanation of the ramifications of the hyperbolic metric can be found in one of the many mathematical textbooks which cover hyperbolic geometry [Mar75] [Wol45].
Figure 5: Left: Parallel lines in euclidean space are always the same distance apart. Middle: In hyperbolic space the distance between two lines that never meet does indeed change. Here we show two geodesics which never meet but are not equidistant: the further they extend away from the origin, the more room there is between them.
When we deal with a single still image, a projection from hyperbolic space looks similar to a euclidean scene projected through a fisheye lens. However, motion of an object constructed with hyperbolic geometry is very different from the motion of a euclidean object. Although we could simply place euclidean objects into hyperbolic 3-space and move them around according to the rules of hyperbolic geometry, we would not be exploiting the exponential amount of room available in hyperbolic space.
Although hyperbolic space is an infinite space more voluminous than
euclidean space, we can project it into a finite volume of euclidean
space. There are two standard projections which map all of hyperbolic
space into a ball in euclidean space. The projective model
preserves straight lines and distorts angles, while the conformal
ball model preserves angles and warps lines. The 2D hyperbolic
browser developed at Xerox PARC uses the conformal ball model
[LRP95]. We use the projective model in our implementation
and in the layout derivation in the Appendix. Transformations in the
3D projective model can be expressed as ![]() matrices, so we use
that model to gain maximum performance. The mapping from projective to
conformal coordinates is straightforward, so our layout algorithm
could be adapted for a conformal browser. A good discussion of
hyperbolic transformations for use in computer graphics can be found
in [PG92], so we do not discuss navigation details in this
paper.
matrices, so we use
that model to gain maximum performance. The mapping from projective to
conformal coordinates is straightforward, so our layout algorithm
could be adapted for a conformal browser. A good discussion of
hyperbolic transformations for use in computer graphics can be found
in [PG92], so we do not discuss navigation details in this
paper.
We show a diagram of a one-dimensional version of the projective model in Figure 5. We project from the hyperbola to a line segment tangent to the pole of the hyperbola that stretches between the asymptotes. Every ray projected from the hyperbola to an eye point at the crossing of the asymptotes will fall on this line segment, which is the image plane. In the one dimensional case, objects are line segments on the hyperbola. Objects near the pole of the hyperbola will be nearly undistorted. Projected rays for objects further away from the pole fall closer and closer together on the line segment. We thus see that rigid translations on the hyperbola result in shrinkage of the projected objects, which can never fall outside the line segment.
Figure 6: An illustration of the projective model for one-dimensional hyperbolic space. The image plane is at the pole of one sheet of the hyperbola and the eye point is where the asymptotes meet. While the projection near the pole is almost undistorted, the apparent shrinkage increases as the rays reach further up the hyperbola.
In the three dimensional case we project from a volume to a
volume![]() .
The analog of the line segment in 1D and the disc in 2D is the unit
ball in three dimensional space. Our hyperbolic volume is a
3-hyperboloid, whose associated objects are the kind of three
dimensional shapes that we usually see in 3D graphics. The same
properties that we saw in the one dimensional case still hold. Objects
at the center of the ball are undistorted. When we translate objects
away from the pole of the 3-hyperboloid their projections grow
smaller. These projections can approach, but never reach, the surface
of the ball.
.
The analog of the line segment in 1D and the disc in 2D is the unit
ball in three dimensional space. Our hyperbolic volume is a
3-hyperboloid, whose associated objects are the kind of three
dimensional shapes that we usually see in 3D graphics. The same
properties that we saw in the one dimensional case still hold. Objects
at the center of the ball are undistorted. When we translate objects
away from the pole of the 3-hyperboloid their projections grow
smaller. These projections can approach, but never reach, the surface
of the ball.
Although the layout described in the Appendix uses hyperbolic distances, we must eventually project to from hyperbolic to euclidean coordinates in order to actually draw a picture with standard low-level graphics libraries. The time at which this conversion takes place has a major impact on the size of the static structure that can be displayed without encountering precision problems. Distinct hyperbolic coordinates which are too far from the origin will be projected so close to the surface of the unit ball that there are not enough bits to distinguish between their euclidean coordinates.
Objects that far from the origin do not need to be rendered, since they would project to an area much smaller than a pixel. The limit only comes into play if we store a static structure in euclidean coordinates that is much larger than the part which is actively being drawn.
In our implementation we do store a static structure: we project immediately after the layout phase, and then change the focus from one part of the structure to another by applying a transformation to the static structure. Nodes which are too far from the current root of the tree are marked as truncated, and can only be seen if the tree is laid out from a closer root. A more sophisticated implementation could defer the projection until render time and dynamically determine the appropriate euclidean coordinates for only objects in the neighborhood around the focus that are large enough to see.
We have implemented the H3 layout technique as part of the SiteMgr application for web site creation and management from Silicon Graphics. Most of the paper as a whole focuses on the layout algorithm, but this section describes key features of the SiteMgr visualization component.
The SiteMgr system allows interactive navigation of structures which are too large to render in their entirety, by providing explicit gardening controls to expand or contract subtrees. The original PARC cone tree system [RMC91] also used explicit gardening, but this approach is inferior to the automatic subtree expansion and collapse featured in systems such as the PARC 2D hyperbolic browser [LRP95] or Carrière's cone tree extension [CK95]. We do automatically cull text labels when nodes move far from the origin.
The user can also toggle the display of nontree links which enter or leave selected nodes. We distinguish incoming from outgoing nontree links to allow fine-grained control of the display. Nodes like logo images tend to have many incoming links, while table of contents nodes would have many outgoing links. Nodes are colored according to MIME type. The user can choose a different root node for the spanning tree, which will show a very different view of the graph.
When the user clicks on a node, it is selected and undergoes an animated transition to the center of the sphere. In addition to this translational component, the transition includes a rotational component so that when the node reaches the origin its ancestors are on its left while its descendants appear on the right. This butterfly representation serves to orient the user and to minimize occlusion of both nodes and their text labels. In the terminology of the original PARC paper [RMC91], we have chosen the horizontal cam trees orientation instead of the vertical cone tree orientation. If the user clicks on an edge, that point is translated to the center of the sphere but no rotation or selection occurs.
The SiteMgr system was designed and tuned for web site visualization. However, it is possible to import graphs into the hyperbolic viewer that were created from other kinds of data, which is how the Unix filesystem and function call graph figures in this paper were made.
The H3 layout technique can easily handle thousands of nodes and has
been tested on graphs of over 20,000 nodes. It is very effective at
presenting a large neighborhood of a huge graph in a small amount of
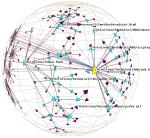
screen space. Plate 1
![]() shows a medium sized Web site which
contains 5000 total nodes. The leftmost image shows a selected node
with outgoing nontree links drawn. Although distant subtrees are quite
distorted, we can see enough context that the destinations of the
non-tree links can be roughly distinguished. In the other two images
we bring the cluster of nodes which contains the destination of most
of the nontree links closer to the focus. Notice that we can still see
the originating node, although it is quite far away in the tree
structure.
shows a medium sized Web site which
contains 5000 total nodes. The leftmost image shows a selected node
with outgoing nontree links drawn. Although distant subtrees are quite
distorted, we can see enough context that the destinations of the
non-tree links can be roughly distinguished. In the other two images
we bring the cluster of nodes which contains the destination of most
of the nontree links closer to the focus. Notice that we can still see
the originating node, although it is quite far away in the tree
structure.
Static pictures such as figures in this paper may be misinterpreted as showing 2D objects on the surface of a hemisphere instead of as 3D objects inside the volume of a ball. In the interactive system the scene is disambiguated as soon as the user sees the objects rotate inside the ball. The interactive user experience is difficult to communicate through still images, but can be approximated with image sequences and the accompanying video.
Hyperbolic methods are very effective at providing global overviews and displaying many nodes at once. We can categorize the drawn nodes into three classes: main/labelled, peripherial, and fringe. What we call peripheral nodes are small but still distinguishable as individual entities upon close inspection. Fringe nodes are not individually distinguishable, but their aggregate presence or absence shows significant structure of far-away parts of the graph. Each class can fit roughly an order of magnitude more than the last. The H3 and PARC browsers can both show up to 50 main/labelled nodes. The PARC layout doesn't have peripheral nodes as such, since nodes are not drawn as discrete entities. The H3 layout can show up to 500 peripheral nodes. The H3 fringe can show information about thousands of nodes, whereas the PARC fringe shows information about hundreds of nodes. (The webviz browser [MB95] didn't have labelled nodes, could handle up to 50 peripheral nodes and show information about up to 500 fringe nodes.)
Another big advantage of moving from a 2D tree to a 3D graph is the ability to see non-tree links in context. One of the greatest strengths of the H3 approach is the ability to see relationships between a part and the far-flung reaches of the whole. Although the details of the nontree link destinations are usually distorted, a rough sense of their direction helps the user construct and maintain a mental model of the overall graph structure. The details become clear in a smooth transition when that area of the structure is brought towards the center. It might be possible to extend a 2D browser to support graph display, but nontree links would have to be drawn in the same plane as the main spanning tree links, necessarily intersecting them. In the 3D system the nontree links can follow paths which are unlikely to intersect the surrounding spanning tree links.
Information density is not the only metric: when taken too far, it
becomes clutter. Going to the third dimension is not a panacea.
Drawing all the links in a highly connected 3D graph yields a picture
which can give a high level overview of the global structure but is
useless for examining the details. The ability to interactively select
which non-tree links are drawn is a major improvement of the SiteMgr
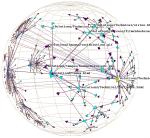
system over the webviz system. Plate 2
![]() shows a function call
graph for a scientific computing benchmark. Such graphs are
notoriously difficult to understand when all the links are drawn.
Software engineers who must modify or optimize unfamiliar code can
browse through the H3 layout of a call graph to understand structure
of a complex program.
shows a function call
graph for a scientific computing benchmark. Such graphs are
notoriously difficult to understand when all the links are drawn.
Software engineers who must modify or optimize unfamiliar code can
browse through the H3 layout of a call graph to understand structure
of a complex program.
The H3 system is very effective at showing aspects of a large graph such as overviews and part/whole relationships that are poorly displayed using other techniques. The converse is that H3 is not well suited for tasks where traditional systems shine, like selecting an item from a linear list. We promote the H3 layout as an additional module to augment other visualization components, not a general-purpose browser that should replace all other views. The SiteMgr system also includes a traditional 2D directory browser to provide an different view. Nodes selected in one browser are automatically highlighted (brushed) in the other, and each can trigger scrolling or an animated transition to the selected document in the other.
The choice of spanning tree has a considerable bearing on the visual impact of the drawn graph. We would like to consider additional heuristics for finding reasonable spanning trees, particularly for domains other than the Web. We are also interested in alternative arrangements of child nodes on parental hemispheres.
We are quite interested in extending the underlying visualization system to allow effortless navigation through huge graphs by automatically expanding subtrees as they approach the center of interest and contracting those that move out to the periphery.
Extremely large graphs will not be understandable if presented only at a single level of detail, even if we had an infrastructure for smooth automatic navigation through millions of nodes. We need to find appropriate abstractions for both graph theoretic structures such as subtrees and for domain-specific structures such as a Web site.
We have presented a new layout technique for visualizing very large directed graphs in 3D hyperbolic space. The H3 technique handles at least two orders of magnitude more data than general graph layout tools. We compute a variation of a cone tree layout based on a spanning tree, and only draw nontree links for selected nodes on demand. In our hyperbolic variation of the cone tree algorithm, we draw a dense neighborhood around the focus of interest by laying out nodes on a spherical cap covering the mouth of the cone rather than its perimeter. We have achieved promising results graphs of tens of thousands of nodes in application domains as the link structure of the Web, Unix file systems, and function call graphs.
We would like to thank François Guimbretière for his ongoing contributions and George Francis, Pat Hanrahan, Eric Hoffman, Stuart Levy, and Al Marden for productive discussions. Anwar Ghuloum of the Stanford SUIF group graciously provided us with the call graph. We also thank the SiteMgr team at Silicon Graphics: Ken Kershner, Greg Ferguson, and Alan Braverman. This work was supported in part by Silicon Graphics, Inc. and the NSF Graduate Research Fellowship Program.
http://www.dur.ac.uk/~dcs3py/pages/work/documents/lit-survey/IV-Survey/.
The H3 layout method operates in two passes: in the bottom-up pass we
find an approximate radius for each hemisphere and in the top-down
pass we place children on the surface of their parent
hemisphere. In this Appendix we present a detailed derivation of the
radius ![]() of a parental hemisphere and the triple
of a parental hemisphere and the triple ![]() needed to place a child hemisphere on the surface of that
parental hemisphere. For each step of the derivation, we show first
the euclidean then the hyperbolic result.
needed to place a child hemisphere on the surface of that
parental hemisphere. For each step of the derivation, we show first
the euclidean then the hyperbolic result.

![]() Bottom-up pass:
We compute a target surface area
Bottom-up pass:
We compute a target surface area ![]() of a
hemisphere at level p by summing the areas of the disks at the
bottom of the child hemispheres at level p+1. This target surface
area is only an approximation for three reasons. First, the surface
area of a spherical cap is greater than the disk on which it lies. (We
use the disk approximation since its area does not depend on the as
yet unknown parental radius
of a
hemisphere at level p by summing the areas of the disks at the
bottom of the child hemispheres at level p+1. This target surface
area is only an approximation for three reasons. First, the surface
area of a spherical cap is greater than the disk on which it lies. (We
use the disk approximation since its area does not depend on the as
yet unknown parental radius ![]() , which we would need to compute the
area of the spherical cap.) Second, even an optimal circle packing of
the disks of the sphere leaves uncovered gaps between the circles.
Third, our circle packing is known to be suboptimal: circles may use
less vertical space than their alloted band allows, and there may be
unused horizontal space in the outermost band. These issues are
discussed in more detail in Section 3.
, which we would need to compute the
area of the spherical cap.) Second, even an optimal circle packing of
the disks of the sphere leaves uncovered gaps between the circles.
Third, our circle packing is known to be suboptimal: circles may use
less vertical space than their alloted band allows, and there may be
unused horizontal space in the outermost band. These issues are
discussed in more detail in Section 3.
All three reasons lead to an estimate which is less than the necessary area. We use an empirically derived area scaling factor to ensure that collisions do not occur. The other parameter in our implementation is the surface area alloted for hemispheres of leaf nodes. The layout would be too dense if the leaf nodes touched, so we generally specify a larger area than a hemisphere that would exactly fit around the geometric representation of a node. These two parameters control the density of the layout.
The euclidean derivation of the target hemisphere surface
area ![]() at level p is straightforward.
at level p is straightforward.
![]() , so
euclidean radius
, so
euclidean radius ![]() would be
would be ![]() .
The relationship between the parent and child hemispheres is
.
The relationship between the parent and child hemispheres is
![]()
where DA is the area of the disk at the bottom of a child hemisphere and n is the number of children at level p+1.
When we use the hyperbolic area formula
![]() ,
the hyperbolic radius of the parental hemisphere is
,
the hyperbolic radius of the parental hemisphere is
![]() .
.
The parent-child relationship becomes
![]()
Figure 7: We find spherical coordinates ![]() and
and ![]() for
placing a child hemisphere on the surface of a parent hemisphere with
radius
for
placing a child hemisphere on the surface of a parent hemisphere with
radius ![]() .
.
![]() Top-down pass: We use the radius
Top-down pass: We use the radius ![]() of the parent hemisphere
to compute the remaining two spherical coordinates
of the parent hemisphere
to compute the remaining two spherical coordinates ![]() and
and
![]() , which specify the position of the child hemisphere at level
p+1. We compute
, which specify the position of the child hemisphere at level
p+1. We compute ![]() and
and ![]() cumulatively, starting from the
pole at the top of the hemisphere. The children are laid out in
concentric bands surrounding the pole at the top of the hemisphere.
The total
cumulatively, starting from the
pole at the top of the hemisphere. The children are laid out in
concentric bands surrounding the pole at the top of the hemisphere.
The total ![]() angle between child n and child n+1
on band j is the sum of the angles
angle between child n and child n+1
on band j is the sum of the angles ![]() and
and
![]() , which depend on the radii
, which depend on the radii ![]() and
and ![]() of
the children.
We need to derive the angle
of
the children.
We need to derive the angle ![]() given some r as in Figure
7. An angle
given some r as in Figure
7. An angle ![]() depends on
depends on ![]() , the radius of
the spherical cap at
, the radius of
the spherical cap at ![]() . When we use the euclidean radius
. When we use the euclidean radius
![]() and the euclidean right-angle triangle
formula we find the euclidean angle
and the euclidean right-angle triangle
formula we find the euclidean angle
![]() .
If we instead use the hyperbolic radius
.
If we instead use the hyperbolic radius
![]() and the hyperbolic right-angle triangle formula we find the hyperbolic
angle
and the hyperbolic right-angle triangle formula we find the hyperbolic
angle
![]()
We substitute ![]() and
and ![]() to obtain our total:
to obtain our total:
![]()
If the cumulative angle ![]() is greater than
is greater than ![]() , we drop down
to the next band j+1 and reset
, we drop down
to the next band j+1 and reset ![]() to 0.
(The very first child is a singular case, since the band is
just a spherical cap.) The
to 0.
(The very first child is a singular case, since the band is
just a spherical cap.) The ![]() angle between a child on one
band and the next depends on the radius
angle between a child on one
band and the next depends on the radius ![]() of the largest child in
band j and the radius
of the largest child in
band j and the radius ![]() of the largest child in band j+1.
In our current circle packing approach, we know that the first child
in each band will have the largest radius, since we lay out the
children in descending sorted order.
of the largest child in band j+1.
In our current circle packing approach, we know that the first child
in each band will have the largest radius, since we lay out the
children in descending sorted order.
We thus need to derive the angle ![]() given some r, as in
the bottom of Figure 7. The euclidean angle
given some r, as in
the bottom of Figure 7. The euclidean angle ![]() corresponding to r is simply
corresponding to r is simply ![]() . We substitute the
hyperbolic formula for right-angle triangles to find
. We substitute the
hyperbolic formula for right-angle triangles to find
![]()
We substitute ![]() and
and ![]() to obtain our total:
to obtain our total:
![]()
Armed with the triple ![]() , we can center the child
hemisphere in the appropriate spot on the parent hemisphere.
, we can center the child
hemisphere in the appropriate spot on the parent hemisphere.
 (QuickTime 263 KB,
MPEG 242 KB)
(QuickTime 263 KB,
MPEG 242 KB)
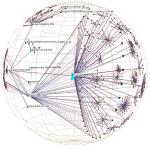
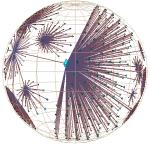
Figure 1: We show part of the Stanford graphics group Web site drawn as a graph in 3D hyperbolic space. The entire site has over 20,000 nodes, of which about 4000 in the neighborhood of the papers archive are drawn here. In addition to the main spanning tree, we draw the nontree outgoing links from an index of every paper by title. The tree is oriented so that ancestors of a node appear on the left and its descendants grow to the right.
Figure 2: We compare the traditional cone tree layout along the circumference of a circle with the H3 layout on the surface of the spherical cap. Both pictures show 54 child nodes in hyperbolic space, represented by pyramids of the same size. Left: The traditional perimeter layout requires a large cone radius and is quite sparse. Right: A quite small cone radius suffices for the H3 spherical cap, so the layout is reasonably dense.
 (QuickTime 277 KB,
MPEG 331 KB)
(QuickTime 277 KB,
MPEG 331 KB)
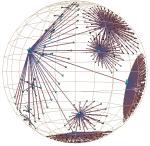
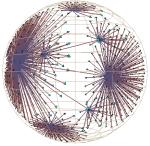
Figure 4: Hyperbolic motion through generations of a 2000-node Unix file system. The sequence begins at the top of the first column and continues at the top of the second. Motion in the first 6 images is mostly translation, while the last two show 3D rotation. The file system has a strikingly large branching factor when compared with the Web sites in Figure 1 or the call graphs in Plate 2. The /dev directory that passes through the focus contains over 200 files.
 (QuickTime 528 KB,
MPEG 225 KB)
(QuickTime 528 KB,
MPEG 225 KB)
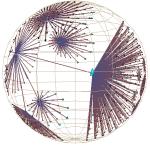
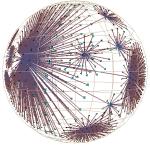
Plate 1: We show the link structure of a Web site laid out in 3D hyperbolic space. The nodes represent documents, which are colored according to MIME type: HTML is cyan, images are purple, and so on. We draw the outgoing non-tree links for the selected node, highlighted in yellow. On the left the destination of those links is quite distorted, but we do see that most of the links end at a particular cluster. The images on the middle and right show that cluster in more detail as we bring it towards the focus.
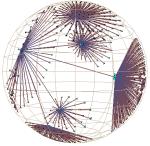
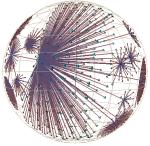
Plate 2: We show the static function call graph structure for a mixed C/FORTRAN scientific computing benchmark. On the left the node coloring indicates whether a particular global variable was untouched (cyan), referenced (blue), or modified (pink). On the right we color by a different variable. Such displays can help software engineers see which parts of a large and/or unfamiliar program might be modularizable.