Image Synthesis: CMPT 761 (Fall 2009)

Instructor: Dr. Torsten Möller

Final Project: An Ocularist's Approach to Human Iris Synthesis

Output of the project: different types of iris renderings

Introduction

In this project I have investigated how PBRT could be used to render human iris using approaches similar to ocularists. An ocularist typically composites many semi-transparent painted layers to create a prosthetic iris. The painted layers look unrealistic by themselves but when they are composited with many other it provides a sense of depth and gives a convincingly realistic look. Lefohn et al. [1] have shown how computer graphics frameworks can be used to synthesize an iris similarly to ocularists. For this project, I have implemented the algorithm proposed by Lefohn et al. [1] with some deviations to allow PBRT to render an iris in reasonable time.

The Rendering Model

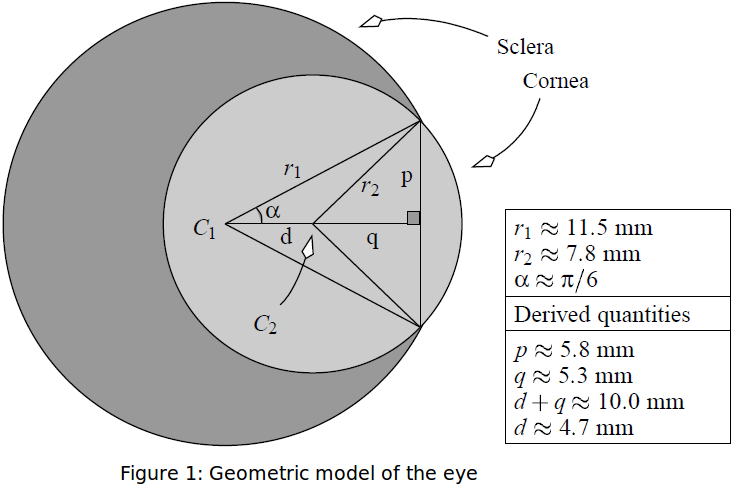
Lefohn et al. [1] proposed a simple geometric model of an eye as depicted in Figure 1. Both sclera and the cornea are modeled using simple spheres whose centers are placed approximately 4.7mm apart. As shown in Figure 1, the part of spheres C2 that sticks out of C1 serves as the cornea. The iris, which is not shown in Figure 1, basically takes the shape of a flat cone frustum, ie. a cone whose apex has been cut off, and sits below the cornea to fill in the circle that is described by the intersection of C1 and C2. In the paper, Lefohn et al. 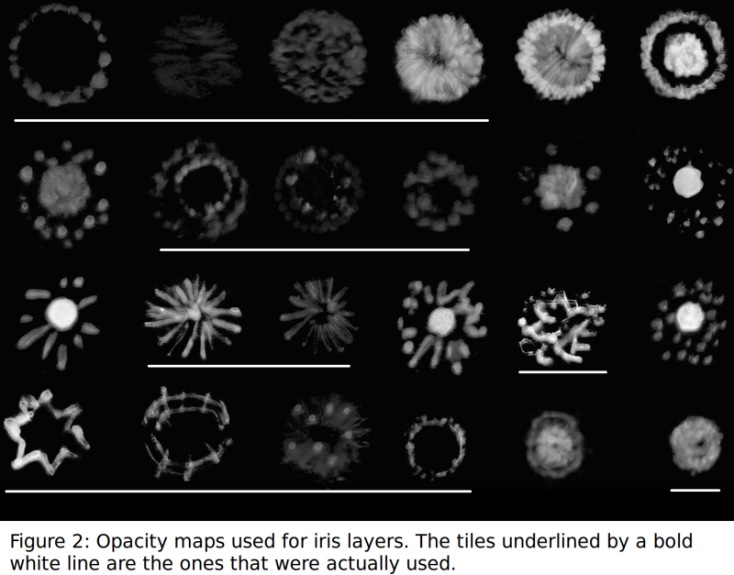[1], proposed to model the iris by stacking several layers of such cone frustums. Each layer of the cone frustum is texture mapped with an opacity map chosen from Figure 2. As suggested by Lefohn et al. [1] , only the tiles that are underlined by a bold white line were actually used. They also did pointed out that the order in which the tiles can be chosen is free. However, in my implementation I have used a probability model to select specific types of tiles more often for a given type of iris (e.g. brown iris compared to blue iris).

Implementation

In the first phase of the implementation I added a shape in PBRT called "conefrustum," which is made by modifying the existing cone shape with its apex chopped off. Extra care had to be taken so that rays which passes through the top hole (where the apex resided in the original cone) can intersect the inner wall. Next I transformed each tile of the pattern texture (see Figure 2) to the u and v parameter space of the cone. The following Figure shows one example of such transformation:

In this Figure, the left hand image gets transformed to the right hand image, which is later used for texturing the conefrustum. To perform this transformation I wrote a simple Matlab script. Next I modeled an iris by stacking several conefrustums, as suggested by Lefohn et al. [1], which are separated from the next one by a small distance. Each conefrustum had a color and a opacity map associated to it. However this approach led to several problems in PBRT. First of all, I had to modify conefrustum so that "IntersectP" method always returns false. This hack was necessary so that, with "directlighting" surface integrator, PBRT doesn't cast shadows on the conefrustums that are below the topmost one. In addition to that, PBRT doesn't attenuate shadow rays based on the opacity maps on the upper layers and this produces a rather unsual image. Due to floating point accuracy two conefrustums cannot be brought too close to each other and visual artifacts are sometimes seen around the pupil (the black dot in the middle of the eye). Finally, with many conefrustum the overall rendering becomes very slow. All these problems led me to decide on modifying the iris rendering model a proposed by Lefohn et al. [1] to something that can be reasonably handled by PBRT. Even though Lefohn et al. [1] proposed stacking conefrustum to model iris, a closer inspection of their rendering equation necessarily suggests an actual volume rendering, which they were approximating using layers of conefrustums. With this insight, I decided to implement a volume rendering technique using multiple textures and opacity to render iris with just one single conefrustum. For this I implemented a new material called "IrisMaterial" which would be associated with the conefrustum that describes the geometry of the iris. Finally to achieve a stronger specular reflection, often termed as catchlights, I hacked the glass material in PBRT to create a new one called "cornea" with the specular reflection being done using Fresnel Conductor added with a Dielectric Microfacet BRDF with roughness parameter set to very low.

IrisMaterial

One major assumption is made while implementing IrisMaterial: the thickness of the overall iris is infinitesimally small. With this assumption, volume rendering can be performed perpendicular to the surface of the iris regardless of the incoming ray direction. However, taking the ray direction into account is an easy extension, which will require changes in the DifferentialGeometry class of PBRT to include a ray direction too. But, on the other hand, infinitesimal thickness of the iris is not a very unfair assumption and this makes implementation rather straightforward. IrisMaterial takes n number of color and opacity textures as parameters and performs volume rendering as illustrated in Figure 3.

Each layer has an opacity "op_i" and color "c_i" maps, while the index (i) is the layer index. Please note that the layer index is counted from 0 to n-1. For each layer we compute transmittance $t_i$ which is given by

.

This also can be written in recurrence form as follows

.

The overall transmittance of the iris T is given by:

.

Therefore by definition the overall opacity O of the iris is given by:

.

With the above definitions, the composite color C of the iris at a given point on the surface is thus given by:

.

Note, due the the recurrence relation shown above, this summation can be terminated early as soon as $t_k = 0$ or very close to 0. A close inspection reveals that this whole scheme is nothing but front-to-back volume rendering. Having the overall composite color C, transmittance T and opacity O, we can derive a BRDF for the iris which is the summation of transmittance, diffuse (lambertian), microfacet and specular BRDFs. The lambertian BRDF takes the overall color C as the argument while the transmittance BRDF take T and a arbitrary refractive index (in my case I used 1.5). Microfacet BRDF takes a roughness parameter, for which I used a very small value (0.01) and specular BRDF takes 1.5 as refractive index. Colors $c_i$ for each layer is chosen by pair wise mixing any two colors from the palette below, as proposed by Lefohn et al. [1]. These colors are blended in HSL space using random blending factor. .

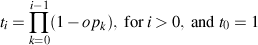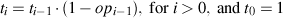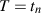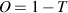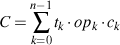Implementation Subtleties

Unfortunately, the opacity maps that I used from the paper are of very low resolution and produce a blurry end image. To circumvent that, I modified the transmittance equation as the following

Here $alpha_i$ (usually greater than 1) scales the opacity $op_i$ and $\beta_i$ is typically greater than 1. This has an effect of sharpening the opacity map and reduce blurriness to some extents. Care must be taking in clamping the values of opacity ( between 0 and 1 ) after scaling or else PBRT may produce a wrong image.

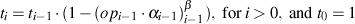Randomly Drawing Layer Patterns and Color

In their paper, Lefohn et al. [1] suggested that layers can be chosen in any order almost randomly. However, they did mention rather casually that for light colored iris, for example blue iris, sharper patterns (with high frequency) are chosen more often by the occularists. On the other hand, for darker iris, for example brown iris, smeared patters are chosen more often. To take these facts into account I designed a probability distribution function for the iris patterns ( see Figure 2 ). For light colored eye, the function is modeled such that high frequency patterns have higher probabilities compared to the smeared one and for darker eye its the opposite. A separate C/C++ program was made that generates a PBRT script for a particular type of iris by taking these probability distribution functions.

Unexpected Difficulties Faced

The main difficulty I faced was to collect the pattern texture. First of all, these pattern textures were taken directly from the paper of Lefohn et al. [1], as they were not available anywhere else, and therefore are in very low resolution. The second problem was; the pattern textures came on a big collage image (see Figure 2) and there would not be any fixed regular tile size that could be used to crop this image to extract the patterns. Each pattern had to be manually fixed so that the "apparent" center of all the patterns match up properly. This took unexpectedly longer time and was a bit frustrating as well. Since the textures were in low resolutions, extra efforts were made to sharpen them from within PBRT (as described above). The other difficulty I faced was to come up with a good probability function for the patterns to generate each type of iris.

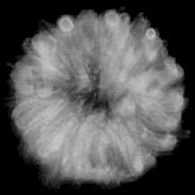
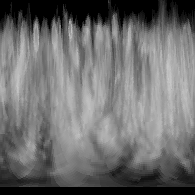
Results

Following are the renditions of different types of iris.

Conclusion

Although my original proposal was about rendering human skin and eye but unfortunately I didn't have the time to do both as I had a very strict TVCG paper deadline. Even more so, a proper skin rendering would also require me to model human face and I have no experience of working with any geometry modeling software. Since I had no group partner and considering the very limited time I had to work on this project I finally decided to do iris rendering only. As far as iris rendering is concerned I believe I have achieved some reasonable quality images. Previously, two more teams have worked on the same problem; one from Stanford and the other one from CMU. In both works, the authors have hand drawn the pattern textures which gave the final image a very synthetic look. Compared to their works, I believe my images look more convincing. The blurriness in my renditions is mainly due to the low resolution pattern textures. With higher resolution images, I believe I could have achieved the same realism as the Lefohn et al. [1].

References

(1) Lefohn, Aaron and Budge, Brian and Shirley, Peter and Caruso, Richard and Reinhard, Erik "An Ocularist's Approach to Human Iris Synthesis"