Geometric Object Generators

A variety of generators for geometric objects are provided in CGAL. They are useful as synthetic test data sets, e.g. for testing algorithms on degenerate object sets and for performance analysis.

The first section provides useful generic functions related to random numbers like random_selection(). The second section documents generators for two-dimensional point sets, the third section for three-dimensional point sets. The fourth section presents examples using functions from Section  to generate composed objects, such as segments. The fifth section describes random convex sets. Note that the STL algorithm std::random_shuffle is useful in this context to achieve random permutations for otherwise regular generators (e.g. points on a grid or segment).

Support Functions for Generators

random_selection()

random_selection chooses $$n items at random from a random access iterator range which is useful to produce degenerate input data sets with multiple entries of identical items.

#include <CGAL/random_selection.h>

template <class RandomAccessIterator, class Size, class OutputIterator, class Random>
OutputIterator	random_selection ( RandomAccessIterator first, RandomAccessIterator last, Size n, OutputIterator result, Random& rnd = default_random)
		chooses a random item from the range $$[first,last) and writes it to result, each item from the range with equal probability, and repeats this $$n times, thus writing $$n items to result. A single random number is needed from rnd for each item. Returns the value of result after inserting the $$n items. Precondition: Random is a random number generator type as provided by the STL or by Random.

2D Point Generators

Two kinds of point generators are provided: first, random point generators and second deterministic point generators. Most random point generators and a few deterministic point generators are provided as input iterators. The input iterators model an infinite sequence of points. The function copy_n() can be used to copy a finite sequence; see Section . The iterator adaptor Counting_iterator can be used to create finite iterator ranges; see Section . Other generators are provided as functions that write to output iterators. Further functions add degeneracies or random perturbations.

Point Generators as Input Iterators

Definition

Input iterators are provided for random points uniformly distributed over a two-dimensional domain (square or disc) or a one-dimensional domain (boundary of a square, circle, or segment). Another input iterator generates equally spaced points from a segment.

All iterators are parameterized with the point type P and all with the exception of the class Points_on_segment_2 have a second template argument Creator, which defaults to the class Creator_uniform_2<double,P>¹. The Creator must be a function object accepting two double values $$x and $$y and returning an initialized point (x,y) of type P. Predefined implementations for these creators like the default can be found in Section . They simply assume an appropriate constructor for type P.

All generators know a range within which the coordinates of the generated points will lie.

#include <CGAL/point_generators_2.h>

Types

The generators comply with the requirements of input iterators, which include local type declarations including value_type, denoted by P here.

Creation

Random_points_in_disc_2<P,Creator> g ( double r, Random& rnd = default_random);
	$$g is an input iterator creating points of type P uniformly distributed in the open disc with radius $$r, i.e. $$|*g| < r . Two random numbers are needed from rnd for each point.

Random_points_on_circle_2<P,Creator> g ( double r, Random& rnd = default_random);
	$$g is an input iterator creating points of type P uniformly distributed on the circle with radius $$r, i.e. $$|*g| == r . A single random number is needed from rnd for each point.

Random_points_in_square_2<P,Creator> g ( double a, Random& rnd = default_random);
	$$g is an input iterator creating points of type P uniformly distributed in the half-open square with side length $$2 a, centered at the origin, i.e. $$ p = *g: -a p.x() < a and $$-a p.y() < a . Two random numbers are needed from rnd for each point.

Random_points_on_square_2<P,Creator> g ( double a, Random& rnd = default_random);
	$$g is an input iterator creating points of type P uniformly distributed on the boundary of the square with side length $$2 a, centered at the origin, i.e. $$ p = *g: one coordinate is either $$a or $$-a and for the other coordinate $$c holds $$-a c < a . A single random number is needed from rnd for each point.

Random_points_on_segment_2<P,Creator> g ( P p, P q, Random& rnd = default_random);
	$$g is an input iterator creating points of type P uniformly distributed on the segment from $$p to $$q (excluding $$q), i.e. $$*g == (1-) p + q where $$0 < 1 . A single random number is needed from rnd for each point. Precondition: The expressions to_double(p.x()) and to_double(p.y()) must result in the respective double representation of the coordinates of $$p, and similarly for $$q.

Points_on_segment_2<P> g ( P p, P q, std::size_t n, std::size_t i = 0);

$$g is an input iterator creating points of type P equally spaced on the segment from $$p to $$q. $$n-i points are placed on the segment defined by $$p and $$q. Values of the index parameter $$i larger than 0 indicate starting points for the sequence further from $$p. Point $$p has index value 0 and $$q has index value $$n-1. Precondition: The expressions to_double(p.x()) and to_double(p.y()) must result in the respective double representation of the coordinates of $$p, and similarly for $$q.

Operations

double

g.range ()

returns the range in which the point coordinates lie, i.e. $$ x: |x| range() and $$ y: |y| range().

The generators Random_points_on_segment_2 and Points_on_segment_2 have two additional methods.

P	g.source ()	returns the source point of the segment.
P	g.target ()	returns the target point of the segment.

See Also

std::random_shuffle, random_selection, copy_n, Counting_iterator, Join_input_iterator_1.

Point Generators as Functions

Grid Points

Grid points are generated by functions that write to output iterators.

template <class OutputIterator, Creator creator>
OutputIterator	points_on_square_grid_2 ( double a, std::size_t n, OutputIterator o, Creator creator = Creator_uniform_2<double,P>)
		creates the first $$n points on the regular $$ sqrt(n) × sqrt(n) grid within the square $$[-a,a] × [-a,a]. Returns the value of $$o after inserting the $$n points. Precondition: Creator must be a function object accepting two double values $$x and $$y and returning an initialized point (x,y) of type P. Predefined implementations for these creators like the default can be found in Section . The OutputIterator must accept values of type P. If the OutputIterator has a value_type the default initializer of the creator can be used. P is set to the value_type in this case.
template <class P, class OutputIterator>
OutputIterator	points_on_segment_2 ( P p, P q, std::size_t n, OutputIterator o)
		creates $$n points equally spaced on the segment from $$p to $$q, i.e. $$ i: 0 i < n: o[i] := (n-i-1)/(n-1) p + (i)/(n-1) q. Returns the value of $$o after inserting the $$n points.

Random Perturbations

Degenerate input sets like grid points can be randomly perturbed by a small amount to produce quasi-degenerate test sets. This challenges numerical stability of algorithms using inexact arithmetic and exact predicates to compute the sign of expressions slightly off from zero.

template <class ForwardIterator>
void	perturb_points_2 ( ForwardIterator first, ForwardIterator last, double xeps, double yeps = xeps, Random& rnd = default_random, Creator creator = Creator_uniform_2<double,P>)
		perturbs the points in the range $$[first,last) by replacing each point with a random point from the xeps $$ × yeps rectangle centered at the original point. Two random numbers are needed from rnd for each point. Precondition: Creator must be a function object accepting two double values $$x and $$y and returning an initialized point (x,y) of type P. Predefined implementations for these creators like the default can be found in Section . The value_type of the ForwardIterator must be assignable to P. P is equal to the value_type of the ForwardIterator when using the default initializer. The expressions to_double((*first).x()) and to_double((*first).y()) must result in the respective coordinate values.

Adding Degeneracies

For a given point set certain kinds of degeneracies can be produced adding new points. The random_selection() function is useful for generating multiple copies of identical points; see Section . The random_collinear_points_2() function adds collinearities to a point set.

template <class RandomAccessIterator, class OutputIterator>
OutputIterator	random_collinear_points_2 ( RandomAccessIterator first, RandomAccessIterator last, std::size_t n, OutputIterator first2, Random& rnd = default_random, Creator creator = Creator_uniform_2<double,P>)
		randomly chooses two points from the range $$[first,last), creates a random third point on the segment connecting these two points, writes it to first2, and repeats this $$n times, thus writing $$n points to first2 that are collinear with points in the range $$[first,last). Three random numbers are needed from rnd for each point. Returns the value of first2 after inserting the $$n points. Precondition: Creator must be a function object accepting two double values $$x and $$y and returning an initialized point (x,y) of type P. Predefined implementations for these creators like the default can be found in Section . The value_type of the RandomAccessIterator must be assignable to P. P is equal to the value_type of the RandomAccessIterator when using the default initializer. The expressions to_double((*first).x()) and to_double((*first).y()) must result in the respective coordinate values.

See Also

std::random_shuffle, random_selection.

Example

We want to generate a test set of 1000 points, where 60% are chosen randomly in a small disc, 20% are from a larger grid, 10% are duplicates points, and 10% collinear points. A random shuffle removes the construction order from the test set. See Figure for the example output.

// generators_prog1.C
// ------------------------------------------
// CGAL example program for point generators.

#include <CGAL/basic.h>
#include <cassert>
#include <vector>
#include <algorithm>
#include <CGAL/Cartesian.h>
#include <CGAL/Point_2.h>
#include <CGAL/point_generators_2.h>
#include <CGAL/copy_n.h>
#include <CGAL/random_selection.h>
#include <CGAL/IO/leda_window.h>  // used for visualization

using namespace CGAL;

typedef Cartesian<double>                R;
typedef Point_2<R>                       Point;
typedef Creator_uniform_2<double,Point>  Creator;
typedef std::vector<Point>               Vector;

int main() {
    // Create test point set. Prepare a vector for 1000 points.
    Vector points;
    points.reserve(1000);

    // Create 600 points within a disc of radius 0.6
    Random_points_in_disc_2<Point,Creator> g( 0.6);
    CGAL::copy_n( g, 600, std::back_inserter(points));

    // Create 200 points from a 15 x 15 grid.
    points_on_square_grid_2(0.95, 200, std::back_inserter(points),Creator());

    // Select 100 points randomly and append them at the end of
    // the current vector of points.
    random_selection( points.begin(), points.end(), 100,
                      std::back_inserter(points));

    // Create 100 points that are collinear to two randomly chosen
    // points and append them to the current vector of points.
    random_collinear_points_2( points.begin(), points.end(), 100,
                               std::back_inserter(points));

    // Check that we have really created 1000 points.
    assert( points.size() == 1000);

    // A random permutation to hide the creation order in the point set.
    std::random_shuffle( points.begin(), points.end(), default_random);

    // Visualize point set.
    leda_window* window = create_and_display_demo_window();
    for( Vector::iterator i = points.begin(); i != points.end(); i++)
        *window << *i;

    // Wait for mouse click in window.
    Point p;
    *window >> p;
    delete window;
    return 0;
}

Figure: Output of example program for point generators.

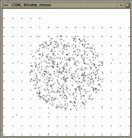
The second example demonstrates the point generators with integer points. Arithmetic with doubles is sufficient to produce regular integer grids. See Figure for the example output.

// generators_prog2.C
// ------------------------------------------------------------------
// CGAL example program for point generators creating integer points.

#include <CGAL/basic.h>
#include <cassert>
#include <vector>
#include <algorithm>
#include <CGAL/Cartesian.h>
#include <CGAL/Point_2.h>
#include <CGAL/point_generators_2.h>
#include <CGAL/copy_n.h>
#include <CGAL/IO/leda_window.h>  // used for visualization

using namespace CGAL;

typedef Cartesian<double>                R;
typedef Point_2<R>                       Point;
typedef Creator_uniform_2<double,Point>  Creator;
typedef std::vector<Point>               Vector;

int main() {
    // Create test point set. Prepare a vector for 400 points.
    Vector points;
    points.reserve(400);

    // Create 250 points from a 16 x 16 grid. Note that the double
    // arithmetic _is_ sufficient to produce exact integer grid points.
    // The distance between neighbors is 34 pixel = 510 / 15.
    points_on_square_grid_2( 255.0, 250, std::back_inserter(points),Creator());

    // Lower, left corner.
    assert( points[0].x() == -255);
    assert( points[0].y() == -255);

    // Upper, right corner. Note that 6 points are missing to fill the grid.
    assert( points[249].x() == 255 - 6 * 34);
    assert( points[249].y() == 255);

    // Create 250 points within a disc of radius 150.
    Random_points_in_disc_2<Point,Creator> g( 150.0);
    CGAL::copy_n( g, 250, std::back_inserter(points));

    // Check that we have really created 500 points.
    assert( points.size() == 500);

    // Visualize point set.
    leda_window* window = create_and_display_demo_window();
    window->init(-262.0, 261.0, -262.0);
    for( Vector::iterator i = points.begin(); i != points.end(); i++)
        *window << *i;

    //  Wait for mouse click in window.
    Point p;
    *window >> p;
    delete window;
    return 0;
}

Figure: Output of example program for point generators working on integer points.

3D Point Generators

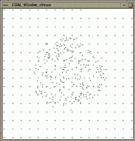
One kind of point generator is currently provided for 3D points: Random point generators implemented as input iterators. The input iterators model an infinite sequence of points. The function copy_n() can be used to copy a finite sequence, see Section . The iterator adaptor Counting_iterator can be used to create finite iterator ranges, see Section .

Point Generators as Input Iterators

Definition

Input iterators are provided for random points uniformly distributed in a three-dimensional volume (sphere or cube) or a two-dimensional surface (boundary of a sphere).

All iterators are parameterized with the point type P and a second template argument Creator which defaults to Creator_uniform_3<double,P>². The Creator must be a function object accepting three double values $$x, $$y and $$z and returning an initialized point (x,y,z) of type P. Predefined implementations for these creators like the default can be found in Section . They simply assume an appropriate constructor for type P.

All generators know a range within which the coordinates of the generated points will lie.

#include <CGAL/point_generators_3.h>

Types

The generators comply with the requirements of input iterators, which include local type declarations including value_type, denoted by P here.

Creation

Random_points_in_sphere_3<P,Creator> g ( double r, Random& rnd = default_random);
	$$g is an input iterator creating points of type P uniformly distributed in the open sphere with radius $$r, i.e. $$|*g| < r . Three random numbers are needed from rnd for each point.

Random_points_on_sphere_3<P,Creator> g ( double r, Random& rnd = default_random);
	$$g is an input iterator creating points of type P uniformly distributed on the boundary of a sphere with radius $$r, i.e. $$|*g| == r . Two random numbers are needed from rnd for each point.

Random_points_in_cube_3<P,Creator> g ( double a, Random& rnd = default_random);
	$$g is an input iterator creating points of type P uniformly distributed in the half-open cube with side length $$2 a, centered at the origin, i.e. $$ p = *g: -a p.x(),p.y(),p.z() < a . Three random numbers are needed from rnd for each point.

See Also

std::random_shuffle, random_selection, copy_n, Counting_iterator, Join_input_iterator_1.

Examples Generating Segments

The following two examples illustrate the use of the generic functions from Section  like Join_input_iterator_2 to generate composed objects from other generators - here two-dimensional segments from two point generators.

We want to generate a test set of 200 segments, where one endpoint is chosen randomly from a horizontal segment of length 200, and the other endpoint is chosen randomly from a circle of radius 250. See Figure for the example output.

// Segment_generator_prog1.C
// -------------------------------
// CGAL example program for the generic segment generator.

#include <CGAL/basic.h>
#include <cassert>
#include <vector>
#include <algorithm>
#include <CGAL/Cartesian.h>
#include <CGAL/Point_2.h>
#include <CGAL/Segment_2.h>
#include <CGAL/point_generators_2.h>
#include <CGAL/function_objects.h>
#include <CGAL/Join_input_iterator.h>
#include <CGAL/copy_n.h>
#include <CGAL/IO/leda_window.h>  // used for visualization

using namespace CGAL;

typedef Cartesian<double>                R;
typedef Point_2<R>                       Point;
typedef Creator_uniform_2<double,Point>  Pt_creator;
typedef Segment_2<R>                     Segment;
typedef std::vector<Segment>             Vector;

int main() {
    // Create test segment set. Prepare a vector for 200 segments.
    Vector segs;
    segs.reserve(200);

    // Prepare point generator for the horizontal segment, length 200.
    typedef  Random_points_on_segment_2<Point,Pt_creator>  P1;
    P1 p1( Point( -0.4, 0), Point( 0.4, 0));

    // Prepare point generator for random points on circle, radius 250.
    typedef  Random_points_on_circle_2<Point,Pt_creator>  P2;
    P2 p2( 1.0);

    // Create 200 segments.
    typedef Creator_uniform_2< Point, Segment> Seg_creator;
    typedef Join_input_iterator_2< P1, P2, Seg_creator> Seg_iterator;
    Seg_iterator g( p1, p2);
    CGAL::copy_n( g, 200, std::back_inserter(segs));

    // Visualize segments.
    leda_window* window = create_and_display_demo_window();
    for( Vector::iterator i = segs.begin(); i != segs.end(); i++)
        *window << *i;

    //  Wait for mouse click in window.
    Point p;
    *window >> p;
    delete window;
    return 0;
}

Figure: Output of example program for the generic segment generator.

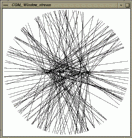
The second example generates a regular structure of 100 segments; see Figure for the example output. It uses the Points_on_segment_2 iterator, Join_input_iterator_2 and Counting_iteratorto avoid any intermediate storage of the generated objects until they are used, which in this example means copied to a window stream.

// Segment_generator_prog2.C
// -------------------------------
// CGAL example program generating a regular segment pattern.

#include <CGAL/basic.h>
#include <algorithm>
#include <CGAL/Cartesian.h>
#include <CGAL/Point_2.h>
#include <CGAL/Segment_2.h>
#include <CGAL/point_generators_2.h>
#include <CGAL/function_objects.h>
#include <CGAL/Join_input_iterator.h>
#include <CGAL/Counting_iterator.h>
#include <CGAL/IO/Ostream_iterator.h>
#include <CGAL/IO/leda_window.h>  // used for visualization

using namespace CGAL;

typedef Cartesian<double>                            R;
typedef Point_2<R>                                   Point;
typedef Segment_2<R>                                 Segment;
typedef Points_on_segment_2<Point>                   PG;
typedef Creator_uniform_2< Point, Segment>           Creator;
typedef Join_input_iterator_2< PG, PG, Creator>      Segm_iterator;
typedef Counting_iterator<Segm_iterator,Segment>     Count_iterator;

int main() {
    // Open window.
    leda_window* window = create_and_display_demo_window();
    window->init(-256.0, 255.0, -256.0);

    // A horizontal like fan.
    PG p1( Point(-250, -50), Point(-250, 50),50);     // Point generator.
    PG p2( Point( 250,-250), Point( 250,250),50);
    Segm_iterator  t1( p1, p2);                       // Segment generator.
    Count_iterator t1_begin( t1);                     // Finite range.
    Count_iterator t1_end( 50);
    std::copy( t1_begin, t1_end, 
               Ostream_iterator<Segment,Window_stream>(*window));

    // A vertical like fan.
    PG p3( Point( -50,-250), Point(  50,-250),50);
    PG p4( Point(-250, 250), Point( 250, 250),50);
    Segm_iterator  t2( p3, p4);
    Count_iterator t2_begin( t2);
    Count_iterator t2_end( 50);
    std::copy( t2_begin, t2_end,
               Ostream_iterator<Segment,Window_stream>(*window));

    // Wait for mouse click in window.
    Point p;
    *window >> p;
    delete window;
    return 0;
}

Figure: Output of example program for the generic segment generator using pre-computed point locations.

Building Random Convex Sets

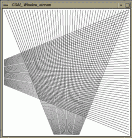
This section describes a function to compute a random convex planar point set of given size where the points are drawn from a specific domain.

#include <CGAL/random_convex_set_2.h>

template < class OutputIterator, class Point_generator, class Traits >
OutputIterator	random_convex_set_2 ( int n, OutputIterator o, Point_generator pg, Traits t = Default_traits)

computes a random convex n-gon by writing its vertices (oriented counterclockwise) to o. The resulting polygon is scaled such that it fits into the bounding box as specified by pg. Therefore we cannot easily describe the resulting distribution.

Precondition

1. Point_generator satisfies the requirements stated in section ,
2. If Traits is specified, it has to satisfy the requirements stated in section and Traits::Point_2 must be the same as Point_generator::value_type,
3. if Traits is not specified, Point_generator::value_type must be Point_2< R > for some representation class R,
4. OutputIterator accepts Point_generator::value_type as value type and
5. $$n 3.

See Also

Implementation

Example

The following program displays a random convex 500-gon where the points are drawn uniformly from the unit square centered at the origin.

#include <CGAL/Cartesian.h>
#include <CGAL/point_generators_2.h> 
#include <CGAL/random_convex_set_2.h>
#include <CGAL/IO/Window_stream.h>
#include <CGAL/IO/Ostream_iterator.h>

int main() {
  typedef Cartesian< double >   R;
  typedef Point_2< R >          Point_2;
  typedef Random_points_in_square_2< 
    Point_2,
    Creator_uniform_2< double, Point_2 > >
  Point_generator;
  
  // create 500-gon and write it into a window:
  Window_stream W;
  W.init( -0.55, 0.55, -0.55);
  random_convex_set_2( 
    500, 
    Ostream_iterator< Point_2, Window_stream >( W),
    Point_generator( 0.5));

  // wait for mouse-click:
  Point_2 p;
  W >> p;
}

• Class declaration of Point_generator.

• Class declaration of Traits.

Footnotes

1	For compilers not supporting these kinds of default arguments, both template arguments must be provided when using these generators.
2	For compilers not supporting these kinds of default arguments, both template arguments must be provided when using these generators.