Foam
By Sean Rosenbaum and Mattias Bergbom
‘‘We live in a universe inundated with foam.’’ - S. Perkowitz
Source
Goal
We intended to render dense foam formations in a physically-correct way. To our knowledge this has never been done (physically-correct). Foam plays such a large role in the appearance of fluids that it is a shame for it not to be taken seriously. We strove to lay some foundation for others to build on.
Related Work
Foam plays a significant part in many petrochemical, biophysical and structural engineering processes, and as such has attracted huge interest from many research fields. For instance, Phelan et al. [1] and Kraynik et al. [2] both use CGAL-based Surface Evolver to compute various geometrical and structural properties in mono-disperse foam. However, little work has been done in visualizing dense foams in a convincing manner. We draw most of our information from the work of Kück et al. [3], who simulate and visualize semi-dense foam using an approximate bubble intersection technique, and Glassner [4], who created double- and triple-bubble formations with physically correct interfaces using CG scripting. Greenwood [5] later improved on Kück's approximations in order to render gas bubbles immersed in liquids in a fluid solver.
Foundation
When we first got started, we knew the bubble intersection geometry and thin-film interference were crucial, regardless of our final solution, so we began working on them immediately. They form the foundation of the brute-force physical model.
Geometry
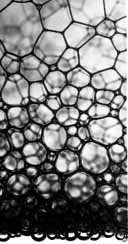
Foam is essentially a collection of gas bubbles enclosed in liquid. The gas-liquid ratio varies, but gas generally dominates in the order of 10 to 1 or more. Each bubble-bubble intersection is a thin wall through which liquid constantly travels under the influence of gravity. Where such walls meet triangular tubes form - called Plateau borders - through which even more liquid is advected. In his legendary work ‘‘Statique expérimentale et théorique des liquides soumis aux seules forces moléculaires’’ Joseph Plateau described how these walls and borders form and meet at very specific angles (namely 120 degrees and 109.47 degrees, respectively).
Glassner [4] uses Plateau's results to derive the optimal distances between pairs and triplets of bubbles, expressed in their respective radii. He also derives a nice expression for the radius and origin of the spherical intersection between two different-sized bubbles. This expression turned out to be both too computationally expensive and a bit excessive when working with dense foams though, so instead we settled for Kück's approximation [3] where the intersection is set to be the parametric average between the two overlapping spherical segments (see figure 1). This gives an illusion of a correctly concave intersection that serves our purposes just fine.
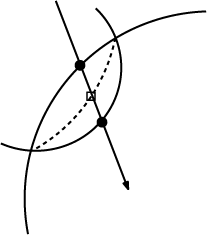
Figure 1. Setting the intersection point to be the halfway point
between the two actual intersection points provides a sufficient
approximation of the physically correct curvature.
Plateau borders, aka. triple bubble intersections, are a different animal. Due to their thickness, they can not be accounted for by the thin film approximation, but should rather be dealt with separately. Having somewhat of a prism-like shape, they provide both in-scattering, out-scattering, dispersion and various other phenomena. Kück [3] models this by letting each Plateau border become a solid, diffuse surface, and adding an ambient term depending on the scene's lights. As Greenwood [5] states though, ‘‘The use of an ambient term for a small bubble cluster is undesirable ... because it is noticeable that light should travel beyond the region where the three spheres overlap’’. As we're striving for flexibility between dense foams and large bubbles, we settle for Greenwood's approximation of averaging the normals between the first and last surfaces entered in the triple-bubble intersection, and setting the hitpoint to the last surface (figure 2). This makes for good-looking big bubble clusters but probably causes a certain loss of scattering in dense foams, and could perhaps have been controlled by a user-provided parameter.
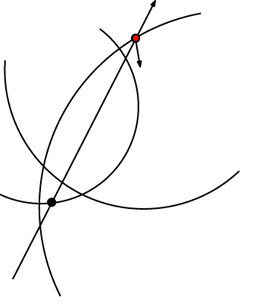
Figure 2. We use the technique proposed by Greenwood [5]
to compute intersection points between three bubbles.
Handling these multiple intersections proved to be somewhat of a hassle. We ended up constructing our own inner loop within the Foam shape's Intersect() method. This loop keeps calling the intersect function of the internal kd-tree storing all the spheres, advancing the ray by increasing its t_min_ parameter, until an actual bubble surface or intersection surface is hit. Then we return the ray as though it had hit its first surface, thereby hiding the sections of the spheres that shouldn't be shown. Slight modifications to the integrator were unfortunately necessary, in order to tell each recursively spawned ray which bubble it's already inside.
The step from doubles and triples to dense foams also provides some challenges. Bubbles are an equilibrium between internal gas pressure and external surface tension. When bubbles interact, there is an intricate balancing act between the repulsive force due to the interest of maintaining a perfectly spherical (and thus minimal) surface, and the attractive force caused by the opportunity to share the separating film and decrease the overall surface area. Added to this dynamic system are the random ruptures in the thin films caused by dust particles in gas and liquid, leaving room for new bubbles to form and keeping the system under constant evolution.
We didn't model these dynamics to any extent, but rather chose to approximate a snap shot of the foam evolution process using various methods. We implemented a combination of a Poisson sampling of the volume of interest (initially a sphere) and a basic relaxation scheme, based on the ideal distances between bubbles as derived by Glassner [4]. Poisson sampling just makes a lot of sense when trying to avoid too-overlapping spheres, whereas the relaxation asserts that the fraction of bubbles not rejected will converge to a nice solution.
As described below, we quite early realized the enormous complexities involved in brute-force rendering tens of thousands - if not more - interfacing bubbles. Instead, we wanted to distribute the brute-force foam as a thin layer on top of whatever reflection model we chose to approximate the internal scattering in the foam. Since pbrt to our knowledge doesn't facilitate a UV-to-triangle mapping, we chose to assume equally sized triangles and uniformly sample among these. Once a triangle has been selected, we sample uniformly over its UV coordinates and finally sample along the interpolated surface normal, factoring in the user-provided thickness. In order to prevent the bubble layer from inflating while relaxing the structure, we also compute the local shading geometry and transform the position vector into tangent space, to detect and remove bubbles that venture too far out of bounds. This helps us avoid the cost of intersection testing against the mesh for each bubble and each relaxation step. For non-smooth objects, we would optimally also compute some kind of a local curvature measure (e.g. by using dn/dp), rather than merely using first derivatives (see figure 3), but in the interest of saving time we assumed our final image would exclusively contain smooth foam objects and thus not be noticeably affected by this type of artifact.
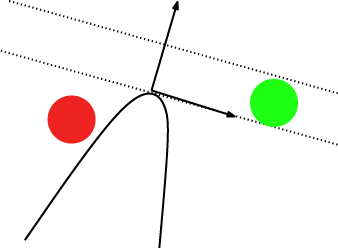
Figure 3. Using local shading geometry to check bubbles against the boundaries doesn't necessarily work for non-smooth surfaces. Here the invalidly positioned green bubble is kept while the correctly placed red bubble is discarded.
Thin-film interference
When light hits the surface of a bubble, there is immediately some reflection, as well as some transmission into the film. The transmitted light hits the inner end of the film where it may reflect again and then once more along the outer boundary, leaving in the same direction as the initial reflection even after accounting for refraction. The light will undergo some phase change, which when combined with the reflection, gives us an interference pattern. Technically there may be many bounces within the film, though we decided to only model the first bounce back as others have done. The main difficulty in implementing thin-film interference is actually extending PBRT to use wavelength in place of the given spectrum representation. Initially we have an RGB 3-tuple for the light that we convert to wavelength using the Fourier-basis conversion described by Glassner [6]. We then compute the interference color using the equations presented in [4], and convert the wavelength back to XYZ and then to RGB.
The image below demonstrates the geometry and interference.
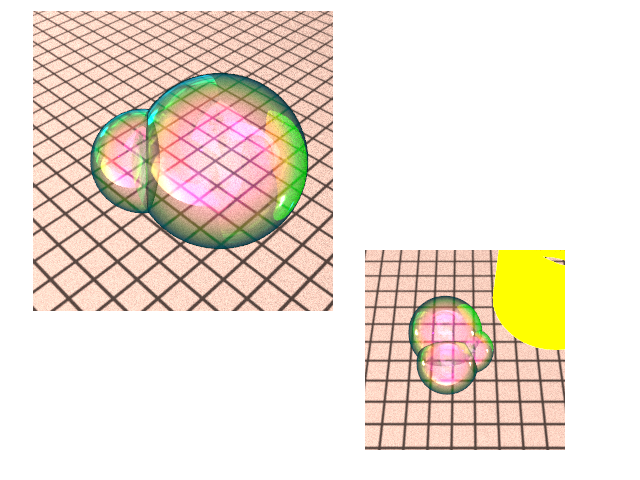
Limitations
Initially we were really excited about tracing rays through the geometric model to develop a pure BSSRDF of the foam (more on that in our conclusions). To our dismay, we realized we were not going to pull it off. Obviously tracing rays through bubble formations is intractable. Each time a ray hits the surface of a bubble, we get two rays, one for the reflection and another for transmission. Even tracing sparse formations in a reasonable amount of time was challenging.

Shell Scattering
We propose a technique we call "shell scattering" which overcomes the recursion limit by only tracing through several layers of geometry, then falling back on a simpler subsurface scattering approximation as we penetrate deeper. This technique enables us to capture the bulk of the optical properties and complexity in a reasonable amount of time.
To achieve this, we had to augment our system with a BSSRDF. We chose to implement Jensen and Buhler's hierarchical subsurface scattering algorithm [7] because of its speed and effectiveness. This algorithm has been implemented a number of times in the past few years by other students, so we will refer the reader to both the paper and the other entries for spurious details. The idea is simply to compute the irradiance at a number of sample points over the mesh with photon mapping or irradiance caching (we used photon mapping). Then a hierarchical structure is built for efficiently computing the contributions from surrounding area for the radiance at a given point. Our implementation consists of a heavily modified PBRT octree. The structure is simply traversed in the manner described by Jensen and Buhler, with an approximation being used when the error is small. The authors suggest Turk's relaxation method be used for sampling the points on the mesh. We found that in practice the vertices, weighted by area, work well as long as the mesh is adequately complex. This was not at all a problem for us since our meshes are fairly smooth and hence adequately sampled. We suspect that in most cases one can get away with this.

The duck on the left is rendered with shell-scattering. Only a BSSRDF is used on the duck on the right.

Shell scattering on a foam-like mesh.
Update: Apparently we are not the only ones using a shell-like model for subsurface scattering. We learned Xin Tong introduced a nearly identical technique in his 2005 SIGGRAPH paper Modeling and Rendering of Quasi-homogeneous Materials .
Conclusion
While we believe we made good progress, it is clear there is more to be done. Sure, one can hack together something that looks like foam using some procedural textures and bump or displacement mapping, but doing it in a physically-correct way is another story, one that we hope you can now appreciate. Our technique dealt with the intractability of the problem in an approximately physically-correct way. In particular, it renders large dense foam formations in high resolution in only a few hours on one of the myth machines, rather than several days on a state-of-the-art 300 machine cluster tracing through all the geometry. Our method fully scatters light, demonstrates geometric complexity and optics, and is relatively fast.
Unfortunately our BSSRDF is incorrect. As we said above, we did not have the resources to trace through dense foam to experimentally derive the scattering and absorption terms. We had no choice but to guesstimate them. In addition, instead of modeling a fixed number of layers, we believe we can reduce the harsh transition between the two models using Russian roulette.
It would also be interesting applying the same idea to other homogeneous translucent bodies. That is, physically modeling layers near the surface, then eventually falling back to a BSSRDF as our rays penetrate deeper.
Extras
We procedurally generated our own biologically-motivated leaf venation patterns. The leaf starts out small, with some point to begin vein growth. We then iteratively grow the veins and the leaf based on the chosen growth model. At each iteration, we expand each vein along the center of mass of nearby auxin-sources. As the veins lengthen, they become fatter. We implemented uniform and marginal growth. In uniform growth, auxin sources are equally likely to be spawned anywhere in the interior of the leaf at each iteration. On the other hand, marginal growth spawns auxin only along the boundary as the leaf is grown. This is based on algorithms described by Runions et al. [9]. After these veins are produced, we overlay the texture with Worley noise [10] for the more complicated tertiary veins exhibited by some plants. We use a grid to accelerate both of these processes. Runions et al. introduced an algorithm to account for the latter sort of veins, but it is very inefficient without more complicated acceleration algorithms being used. We were satisfied with Worley textures and felt they would save us some time. Here is a visualization of this process.

Venation texture used as a bump-map in a scene rendered in Blender.
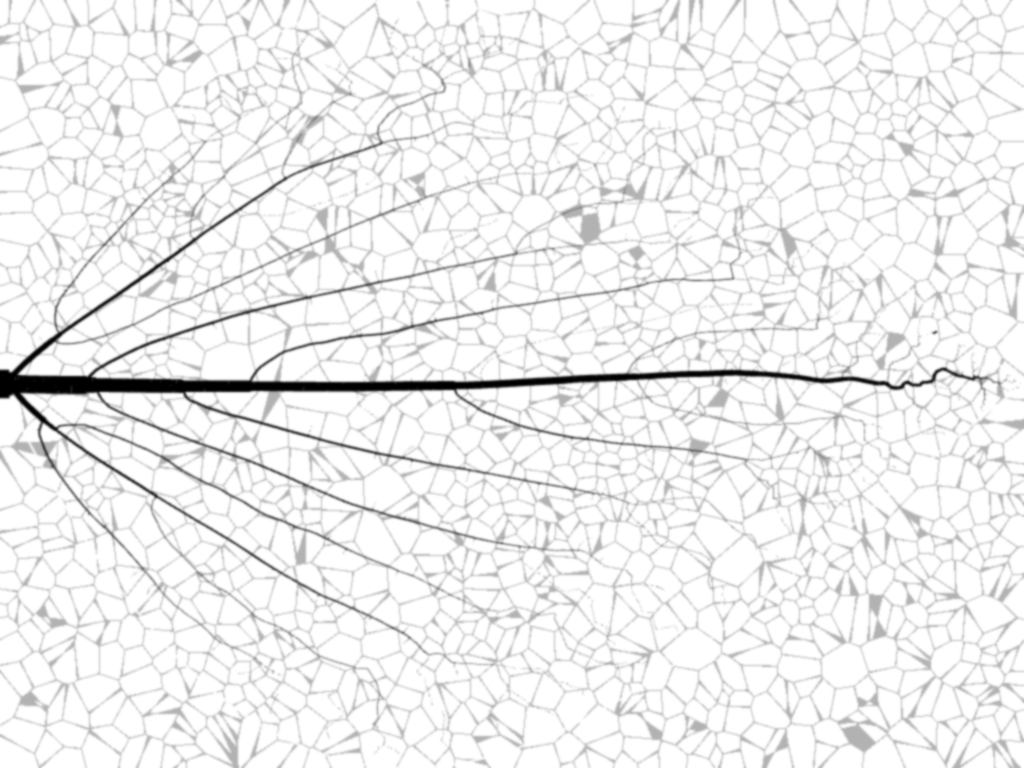
Procedurally generated venation texture.
We initially intended to use these textures as bump-maps, but we had trouble getting the texture coordinates of our leaf models loaded properly in PBRT, so we ended up using the texture as a displacement map in 3D Studio, then exporting the geometry. The final scene we demoed did a rather bad job of demonstrating these textures because there is a lot of light all over the scene and the resolution was not very high. We probably also should have used more displacement to exaggerate them a little. The leaf model was rendered with a mix of our BSSRDF to account for internal scattering and a Lambertian BRDF for the roughness of the surface of leaves. We found this "hack" enabled us to get some interesting translucency while having a rough surface. It also has the advantage of working well if you want to apply bump maps when Jensen's hierarchical algorithm is used.
We also spent a few days dabbling with fluid-simulation. Specifically, we extended the 2D fluid simulator presented by Stam [11] to 3D with arbitrary boundaries. In order to add arbitrary 3D boundaries, we had to voxelize the world. We specify some point in the scene that identifies which volume should be filled to distinguish between the visible world and the inside of a mesh. We then came up with a flood-fill-like algorithm that radiates out from the grid at the chosen point, determining whether or not it is a boundary by shooting a ray in that grid's direction to check for intersection with objects in the scene. Otherwise, extending the simulation to 3D was pretty straightforward.

Magic Ball. Demonstrates boundary awareness.
To make steam, we spawned density along the surface of the volume and added some buoyancy force there. We also applied a general force to uniformly push the fluid in the volume to account for gravity, wind, and so on. We then go through several iterations, continually adding density along the surface as it dissipates, to physically simulate the effect.

Steamy Bubble. The artifacts at the edges result from making the volume smaller than the scene in view.
Final Scene

Lessons Learned
1) Technology is only one factor
We spent an enormous amount of time developing all the technology for rendering foam and some other things in the scene. Consequently, we did not have much time to put things together in the final image; however, we did manage to quickly put something together we were happy with. We ended up starting the render at the last minute and had to exclude the steam because it slowed the rendering down tremendously. We also did not realize the leaf patterns were not showing up well until a few hours prior to the demo and proceeded regardless. The lighting, as well, was problematic. Environmental lighting often washes out translucent material and makes it look more uniform when the lighting does not vary that significantly. Our final image suffered as a result of these issues.
2) Experimentation is costly
Since this problem was largely unexplored, we had to develop our own solution. As stated above, we experimented a great deal - and experimentation of course is a major time sink. And again, we sought to do things physically-correct, which we found made things extremely difficult. To be honest, we may have been able to produce a prettier image with a lot less effort using some noise functions for rendering very dense formations, though as we said, this sort of thing was not our goal. This made producing a pretty picture immensely more challenging for us, though we feel it looks impressive nonetheless!
References
[1] Robert Phelan, Denis Weaire, and Kenneth Brakke. "Computation of equilibrium foam structures using the Surface Evolver". Experimental Mathematics, 4:181--192, 1995.
[2] Andrew M. Kraynik, Douglas A. Reinelt, and Frank van Swol. "Structure of random monodisperse foam". Phys. Rev. E 67, 031403, 2003.
[3] Hendrik Kück, Christian Vogelgsang, and Gunter Greiner. "Simulation and Rendering of Liquid Foams". In Proceedings of Graphics Interface, pages 81--88, May 2002.
[4] Andrew Glassner. "Soap Bubbles: Part 2". IEEE 2000.
[5] Shannon T. Greenwood. "The incorporation of bubbles into a computer graphics fluid simulation". Texas A&M, 2004.
[6] Andrew Glassner. "How to derive a spectrum from an RGB triplet". IEEE 1989.
[7] Henrik Wann Jensen and Juan Buhler. "A rapid hierarchical rendering technique for translucent materials". SIGGRAPH 2002.
[8] Henrik Wann Jensen, Stephen R. Marschner, Marc Levoy, and Pat Hanrahan. "A Practical model for subsurface light transport". SIGGRAPH 2001.
[9] Adam Runions, Martin Fuhrer, Brendan Lane, Pavol Federl, Anne-Gaëlle Rolland-Lagan and Przemyslaw Prusinkiewicz. "Modeling and visualization of leaf venation patterns". SIGGRAPH 2005
[10] Steven Worley. "A cellular texture basis function". SIGGRAPH 1996.
[11] Jos Stam. "Real-Time Fluid Dynamics for Games". Game Developer Conference 2003.
[12] Jos Stam. "Stable Fluids". SIGGRAPH 1999.
Division of Labor
We split the project into two parts: general rendering and bubble geometry, formation, and intersection. This allowed each of us to specialize in a particular area. We were in constant communication and worked out the general direction of the project together.
Sean Rosenbaum
Thin-Film Interference
Hierarchical Subsurface Scattering
Venation Patterns
Steam Simulator
Mattias Bergbom
Bubble Geometry and Intersection
Foam Relaxation
Bubble Sampling Meshes