You are not allowed to do AttachFile on this page. Login and try again.

Assignment 3: Camera Simulation

Due: Tuesday May 8th, 11:59PM

Please add a link to your final writeup on Assignment3Writeups.

Description

Most rendering systems generate images where the entire scene is in sharp focus, thereby mimicking the imaging performance of a pinhole camera. In contrast, real cameras contain multi-lens assemblies with finite apertures and exhibit different imaging characteristics such as limited depth of field, field distortion, vignetting and spatially varying exposure. In this assignment, you'll extend pbrt with support for a more realistic camera model that accurately simulates these effects. Specifically, we will provide you with specifications of real wide-angle, normal and telephoto lenses, each composed of multiple lens elements. You will build a camera plugin for pbrt that simulates the traversal of light through these lens assemblies onto the film plane of a virtual camera. With this camera simulator, you'll explore the effects of focus, aperture and exposure. Once you have a working camera simulator, you will add simple auto-focus capabilities to your camera.

Step 1: Background Reading

Before beginning this assignment you should read the paper "A Realistic Camera Model for Computer Graphics" by Kolb, Mitchell, and Hanrahan. This paper is one of the assigned course readings. You may also want to review parts of Chapter 6 in pbrt.

Step 2: Getting Up and Running

Starter code and data files for Assignment 3 are located at http://graphics.stanford.edu/courses/cs348b-07/assignment3/assignment3.zip. In addition to source, this archive contains pbrt scene you will render in this assignment, a collection of lens data files (.dat), and auto-focus zone info files (.txt).

Modify pbrt

You'll need to make several modifications to pbrt before building the realistic camera plugin. First, add the following virtual method to pbrt's Camera class in core/camera.h.

virtual void AutoFocus(Scene* scene) { }

Next, you'll need to call the AutoFocus method from Scene::Render in core/scene.cpp. Add the following line immediately following the calls to perform surface and volume integrator preprocessing.

camera->AutoFocus(this);

Lastly, you'll need to export the Sample object from pbrt's core shared library. Modify the definition of Sample in core/sampling.h to look like:

struct COREDLL Sample {

Building the camera simulator plugin

Your camera simulator will build into a pbrt plugin named realistic.so (or realistic.dll on Windows). We've included a Makefile for the myth machines as well as a Visual Studio project file. The Visual Studio project assumes it is placed in the same directory as the other pbrt projects (win32/Projects) and that the project source files are placed in the cameras subdirectory of the pbrt source tree. If you wish to place the files elsewhere you will need to modify the project. Linux users may extract the archive to any location, and the build process should work fine as long as PBRT_BASEPATH is set appropriately at the top of the Makefile. Note that the Makefile copies the resulting shared object binary into your pbrt bin directory so no modifications need to be made to your environment's LD_LIBRARY_PATH.

Browse the starter code

In this assignment will implement the RealisticCamera class defined in realistic.cpp. The other files provided in the archive are helper classes that are useful when implementing auto-focus, and are discussed in the auto-focus detail below.

Step 3: Setup the Camera

Notice that the pbrt scenes specify that rendering should use the "realistic" camera plugin. The realistic camera accepts a number of parameters via the scene file, including: the name of a lens data file, the distance between the film plane and the location of the back lens element (the one closest to the film), the diameter of the aperture stop, and the length of the film diagonal (distance from top left corner to bottom right corder of the film). The values of these parameters are passed in to the constructor of the RealisticCamera class. All values are in units of millimeters.

Camera "realistic" 
        "string specfile" "dgauss.50mm.dat" 
        "float filmdistance" 36.77
        "float aperture_diameter" 17.1
        "float filmdiag" 70 

The .dat files included with the starter code describe camera lenses using the format described in Figure 1 of the Kolb paper. RealisticCamera must read and parse the specified lens data file. In pbrt, a camera's viewing direction is the positive z-direction in camera space. Therefore, your camera should be looking directly down the z-axis. The first lens element listed in the file (the lens element closest to the world, and farthest from the film plane) should be located at the origin in camera space with the rest of the lens system and film plane extending in the negative-z direction.

Each line in the file contains the following information about one spherical lens interface.

lens_radius  z-axis_intercept  index_of_refraction  aperture

More precisely:

• lens_radius: is the spherical radius of the element.

• z_axis_intercept: is thickness of the element. That is, it's the distance along the z-axis (in the negative direction) that separates this element from the next.

• index of refraction: is the index of refraction on the camera side of the interface.

• aperture: is the aperture of the interface (rays that hit the interface farther than aperture/2 from the origin don't make it through the lens element)

Note that exactly one of the lines in the data file will have lens_radius = 0. This is the aperture stop of the camera. It's maximum size is given by the aperture value on this line. The actual size of the aperture stop is given as a parameter to the realistic camera via the pbrt scene file. Also note that the index of refraction of the world side of the first lens element is 1 (it's air).

Step 4: Generate Camera Rays

• You now need to implement the RealisticCamera::GenerateRay function. GenerateRay takes a sample position in image space (given by sample.imageX and sample.imageY) as an argument and should return a random ray from the camera out into the scene. To the rest of pbrt, your camera appears as any other camera: Given a sample position it returns a ray from the camera out into the world.

• Compute the position on the film plane that the ray intersects from the values of sample.imageX and sample.imageY

• The color of a pixel in the image produced by pbrt is proportional to the irradiance incident on a film pixel (think of the film as a sensor in a digital camera). This value is an estimate of all light reaching this pixel from the world and through all paths through the lens. As stated in the paper, computing this estimate involves sampling radiance along this set of paths. The easiest way to sample all paths is to fire rays at the back element of the lens and trace them out of the camera by computing intersections and refractions at each lens interface (You will not be using the thick lens approximation from the paper to compute the direction of rays exiting the lens). Note that some of these rays will hit the aperture stop and terminate before exiting the front of the lens.

• GenerateRay returns a weight for the generated ray. The radiance incident along the ray from the scene is modulated by this weight before adding the contribution to the Film. You will need to compute the correct weight to ensure that the irradiance estimate produced by pbrt is unbiased. That is, the expected value of the estimate is the actual value of the irradiance integral. Note that the weight depends upon the sampling scheme used.

• Render each of the four scenes (hw3_dgauss.pbrt, hw3_wide.pbrt, hw3_fisheye.pbrt, hw3_telephoto.pbrt) using your realistic camera simulator. Example images rendered with 512 samples per pixel are given below: telephoto (top left), double gauss (top right), wide angle (bottom left) and fisheye (bottom right). Notice that the wide angle image is especially noisy -- why is that? Hint: look at the ray traces at the top of this web page.

4 samples per pixel

512 samples per pixel

Hints

1. ConcentricSampleDisk() is a useful function for converting two 1D uniform random samples into a uniform random sample on a disk. See p. 270 of the PBRT book.

2. You'll need a data structure to store the information about each lens interface as well as the aperture stop. For each lens interface, determine how to test for intersection and how to determine how rays refract according to the change of index of refraction on either side (review Snell's law).
3. For rays that terminate at the aperture stop, return a ray with a weight of 0 -- pbrt tests for such a case and will terminate the ray instead of sending it out into the scene.
4. Pay attention to the coordinate system used to represent rays. Confusion between world space and camera space can be a major source of bugs.
5. As is often the case in rendering, your code won't produce correct images until everything is working just right. Try to think of ways that you can modularize your work and test as much of it as possible incrementally as you go. Use assertions liberally to try to verify that your code is doing what you think it should at each step. It may be worth your time to produce a visualization of the rays refracting through your lens system as a debugging aid (compare to those at the top of this web page).

Step 5: Play with exposure and depth of field

• Render a second image of the scene using the telephoto lens with the aperture radius reduced by one half. What effects (name two) do you expect to see? Does your camera simulation produce this result? By decreasing the aperture radius by 1/2, how many stops have you decreased the resulting photographs exposure by?

Step 6: Auto-focus

The auto-focus mechanism in a modern digital camera samples light incident on subregions of the sensor (film) plane and analyzes light in these subregions to compute focus. These regions of the frame are called auto-focus zones (AF zones). For example, an auto-focus algorithm might look for the presence of high frequencies (sharp edges in the image) within an AF zone to signal the presence of an in focus image. You most likely have noticed the AF zones in the viewfinder of your own camera. As an example, the AF zones used by the auto-focus system in the Nikon D200 are shown below.

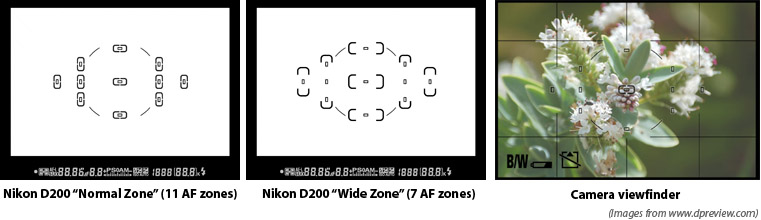
In this part of the assignment, we will provide you a scene and a set of AF zones. You will need to use these zones to automatically determine the film depth for your camera so that the scene is in focus. Notice that in hw3_afdgauss_closeup.pbrt, the camera description contains an extra parameter af_zones. This parameter specifies the text file that contains a list of AF zones. Each line in the file defines the bottom left and top right of a rectangular zone using 4 floating point numbers:

xleft xright ytop ybottom

These coordinates are relative to the top left corner of the film (the numbers will fall between 0.0 and 1.0). For example, a zone spanning the entire film plane would be given by 0.0 1.0 0.0 1.0. A zone spanning the top left quadrant of the film is 0.0 0.5 0.0 0.5.

Implementing Auto-focus

You will now need to implement the AutoFocus method of the RealisticCamera class. In this method, the camera should modify it's film depth so that the scene is in focus.

There are many ways to go about implementing this part of the assignment. One approach is to shoot rays from within AF zones on the film plane out into the scene (essentially rendering a small part of the image), and then analyze the subimage to determine if that part of the image is in focus. The provided assignment 3 starter code is intended to help you implement auto-focus in this manner. Here are some tips to get started with the provided code:

• The provided CameraSensor class is similar to the pbrt Film class but does not write data to files and can be cleared using the Reset() method. You can use this class to produce subimages corresponding to each AF Zone. The CameraSensor::ComputeImageRGB() method will return a pointer to an array of floating point RGB values suitable for analysis.

• SimpleStratifiedSampler is a modified version of PBRT's Stratified sampler plugin that is adapted for the needs of this project. Unlike pbrt's samplers, the SimpleStratefiedSamplercan be reset and reused multiple times.

• Take a look at the "Sum-Modified Laplacian" operator described in Sree Nayar's "Shape From Focus" paper (http://graphics.stanford.edu/courses/cs348b-06/homework3/Nayar_CVPR92.pdf) as an example of a sharpness heuristic.

Test your auto-focusing algorithm, we provide three scenes that require the camera to focus using a single AF zone. The images resulting from proper focusing on hw3_afdgauss_closeup.pbrt, hw3_afdgauss_bg.pbrt, and hw3_aftelephoto.pbrt are shown below (rendered at 512 samples per pixel). The location of the AF zone in each image is shown as a white rectangle.

More advanced auto-focus (not required)

We have also provided scenes hw3_afspheres.pbrt and hw3_bunnies.pbrt that are constructed so that there is a choice of which object to bring into focus and provide multiple auto-focus zones for these scenes. How might you modify your auto-focus algorithm to account for input from multiple zones? Many cameras choose to focus on the closest object they can bring into focus or have "modes" that allow the user to hint at where focus should be set. For example, you might want to add an additional parameter to your camera that designates whether to focus on close up or far away objects in the scene.

More auto-focusing hints

• When generating subimages corresponding to the AF Zones, it will be important that you use enough samples per pixel to reduce noise that may make it difficult to determine the sharpness of the image. By experimentation, we've found that 256 total samples (16x16) using the Sum-Modified Laplacian gives stable results.
• Although the auto-focusing approach described here involves analyzing the image formed within each AF zone, an alternative approach would be to compute an initial estimate of focus using the depth information of camera ray intersections with scene geometry. Using the thick lens approximation from the Kolb paper, you might be able to compute focus more efficiently than the approach described thus far.

• Note that the CameraSensor contains (commented out) code to dump the current image to disk. This can be very useful in debugging.

• Challenge! See how fast and how robust you can make your auto-focusing algorithm. How might you minimize the number of times you re-render a zone? How can you limit the range of film depths you search over? Can you think of better heuristics than the Sum-Modified Laplacian to estimate sharpness?

Step 7: Submission

• We've created wiki pages (FirstnameLastname/Assignment3) for all students in the class. Access to these pages is set up so that only you can view your page. Please compose your writeup on this page and link to it from the Assignment3Writeups page. Your writeup should consist of at least the following:

• A detailed description of your camera implementation and auto-focus algorithm. Be sure to let us know what you tried, what worked well, and what did not work so well. Also describe how you chose to sample paths of light incident on the film through the lens.
• Answer the following questions (please be clear and precise in your answers):
  1. What radiometric quantity is pbrt computing in your camera simulation? In other words: the color of each pixel in the output image is proportional to what quantity?
  2. Write an integral expression to compute the quantity described in question 1 at a point X on the film plane. Please precisely define all variables.
  3. Describe the domain of integration from question 2.

  4. Give the formula for F_n, a Monte Carlo estimator for the value of your integral. F_n is an estimate of the value of the integral using n samples drawn from the domain described in question 3.

  5. How did you draw samples from the domain of integration? Are you certain that you sampled from the space of all paths that light may have traveled through the lens? Describe the probability distribution used to generate random samples.

  6. Describe how pbrt computes F_n using your RealisticCamera class.

• List the film depths computed by your auto-focus algorithm on the various scenes.
• A total of 10 images are required to be submitted in EXR format as attachments to your wiki page. (Feel free to include png or jpg versions of the image inline in your writeup).
  • hw3_dgauss.pbrt, hw3_wide.pbrt, hw2_fisheye.pbrt, hw2_telephoto.pbrt should be rendered at both 4 and 512 samples per pixel.
  • hw3_telephoto.pbrt should be rerendered with the aperture decreased to half the size (render at 512 samples per pixel).
  • hw3_afdgauss_closeup.pbrt, hw3_dgauss_bg.pbrt, hw3_aftelephoto.pbrt should be rendered at the film depth computed by your auto-focus routine with at least 256 samples per pixel.

• Submit your modified realistic.cpp as an attachment to the wikipage. You are free to modify anything in pbrt as long as you submit (or describe) these modifications.

• Please submit any other images you generated and let us know what other cool things you did!

Grading

This assignment will be graded on a 4 point scale:

• 1 point: Significant flaws in camera simulation.
• 2 points: Camera simulation works (or contains minor flaws), no implementation of auto-focus.
• 3 points: Code correct but writeup does not address all points listed above.
• 4 points: Code produces the 9 required images correctly and your writeup addresses all points above.