Abstract

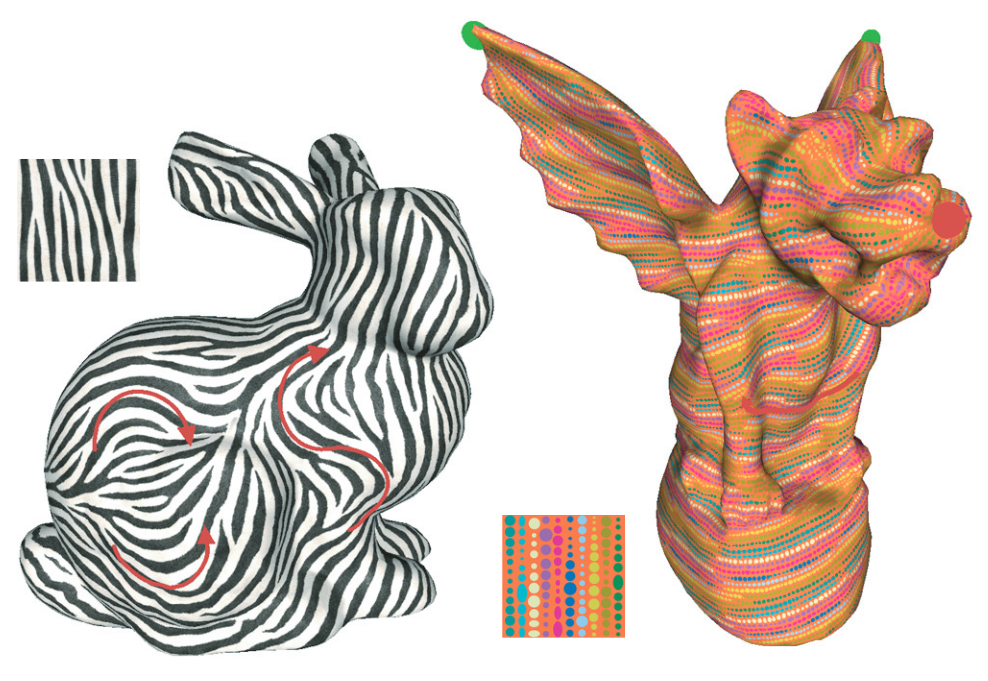
Tangent vector fields are an essential ingredient in controlling surface appearance for applications ranging from anisotropic shading to texture synthesis and non-photorealistic rendering. To achieve a desired effect one is typically interested in smoothly varying fields that satisfy a sparse set of user-provided constraints. Using tools from Discrete Exterior Calculus, we present a simple and efficient algorithm for designing such fields over arbitrary triangle meshes. By representing the field as scalars over mesh edges (i.e., discrete 1-forms), we obtain an intrinsic, coordinate-free formulation in which field smoothness is enforced through discrete Laplace operators. Unlike previous methods, such a formulation leads to a linear system whose sparsity permits efficient pre-factorization. Constraints are incorporated through weighted least squares and can be updated rapidly enough to enable interactive design, as we demonstrate in the context of anisotropic texture synthesis.

Extras

Paper: PDF

Google Scholar: