| bool |
TOPSORT(graph G, node_array<int>& ord) |
| |
|
TOPSORT takes as argument a directed graph G(V, E). It sorts G topologically
(if G is acyclic) by computing for every node v 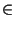 V an integer ord[v]
such that
1 < = ord[v] < = | V| and
ord[v] < ord[w] for all edges
(v, w) V an integer ord[v]
such that
1 < = ord[v] < = | V| and
ord[v] < ord[w] for all edges
(v, w) 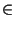 E. TOPSORT returns true if G is acyclic and false otherwise.
The algorithm ([44]) has running time
O(| V| + | E|). E. TOPSORT returns true if G is acyclic and false otherwise.
The algorithm ([44]) has running time
O(| V| + | E|).
|
| list<node> |
DFS(graph G, node s, node_array<bool>& reached) |
| |
|
DFS takes as argument a directed graph G(V, E), a node s of G and a
node_array reached of boolean values. It performs a depth first search
starting at s visiting all reachable nodes v with
reached[v] = false.
For every visited node v
reached[v] is changed to true. DFS returns the
list of all reached nodes.
The algorithm ([76]) has running time
O(| V| + | E|).
|
| list<edge> |
DFS_NUM(graph G, node_array<int>& dfsnum, node_array<int>& compnum) |
| |
|
DFS_NUM takes as argument a directed graph G(V, E). It performs a
depth first search of G numbering the nodes of G in two different ways.
dfsnum is a numbering with respect to the calling time and compnum a
numbering with respect to the completion time of the recursive calls. DFS_NUM
returns a depth first search forest of G (list of tree edges).
The algorithm ([76]) has running time
O(| V| + | E|).
|
| list<node> |
BFS(graph G, node s, node_array<int>& dist) |
| |
|
BFS takes as argument a directed graph G(V, E),a node s of G and
a node array dist of integers. It performs a breadth first search starting
at s visiting all nodes v with
dist[v] = - 1 reachable from s.
The dist value of every visited node is replaced by its distance to s.
BFS returns the list of all visited nodes.
The algorithm ([52]) has running time
O(| V| + | E|).
|
| list<node> |
BFS(graph G, node s, node_array<int>& dist, node_array<edge>& pred) |
| |
|
performs a bread first search as described above and computes for every node
v the predecessor edge pred[v] in the bfs shortest path tree.
|
| int |
COMPONENTS(graph G, node_array<int>& compnum) |
| |
|
COMPONENTS takes a graph G(V, E) as argument and computes the connected
components of the underlying undirected graph, i.e., for every node v 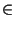 V
an integer
compnum[v] from
[0...c - 1] where c is the number of
connected components of G and v belongs to the i-th connected
component iff
compnum[v] = i. COMPONENTS returns c.
The algorithm ([52]) has running time
O(| V| + | E|). V
an integer
compnum[v] from
[0...c - 1] where c is the number of
connected components of G and v belongs to the i-th connected
component iff
compnum[v] = i. COMPONENTS returns c.
The algorithm ([52]) has running time
O(| V| + | E|).
|
| int |
STRONG_COMPONENTS(graph G, node_array<int>& compnum) |
| |
|
STRONG_COMPONENTS takes a directed graph G(V, E) as argument and computes for
every node v 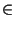 V an integer
compnum[v] from
[0...c - 1] where
c is the number of strongly connected components of G and
v belongs to the i-th strongly connected component iff
compnum[v] = i.
STRONG_COMPONENTS returns c.
The algorithm ([52]) has running time
O(| V| + | E|). V an integer
compnum[v] from
[0...c - 1] where
c is the number of strongly connected components of G and
v belongs to the i-th strongly connected component iff
compnum[v] = i.
STRONG_COMPONENTS returns c.
The algorithm ([52]) has running time
O(| V| + | E|).
|
| int |
BICONNECTED_COMPONENTS(graph G, edge_array<int>& compnum) |
| |
|
BICONNECTED_COMPONENTS computes the biconnected components
of the undirected version of G. A biconnected component of an
undirected graph is a maximal biconnected subgraph and a biconnected
graph is a graph which cannot be disconnected by removing one of its
nodes. A graph having only one node is biconnected.
Let c be the
number of biconnected component and let c' be the number of
biconnected components containing at least one edge, c - c' is the
number of isolated nodes in G, where a node v is isolated if is
not connected to a node different from v (it may be incident to
self-loops). The function returns c and labels each edge of G
(which is not a self-loop) by an integer in
[0...c' - 1]. Two edges
receive the same label iff they belong to the same biconnected
component. The edge labels are returned in compnum. Be aware that
self-loops receive no label since self-loops are ignored when
interpreting a graph as an undirected graph.
The algorithm
([18]) has running time
O(| V| + | E|).
|
| graph |
TRANSITIVE_CLOSURE(graph G) |
| |
|
TRANSITIVE_CLOSURE takes a directed graph G(V, E) as argument and computes
the transitive closure of G(V, E). It returns a directed graph G'(V', E')
with V' = V and
(v, w) 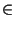 E' E'  there is a path from
v to w in G.
The algorithm ([36]) has running time
O(| V|*| E|). there is a path from
v to w in G.
The algorithm ([36]) has running time
O(| V|*| E|).
|