3 Volumetric integration

Our algorithm employs a continuous implicit function, , represented by samples. The function we represent is the weighted signed distance of each point to the nearest range surface along the line of sight to the sensor. We construct this function by combining signed distance functions , , ... and weight functions , , ... obtained from range images 1 ... n. Our combining rules give us for each voxel a cumulative signed distance function, , and a cumulative weight . We represent these functions on a discrete voxel grid and extract an isosurface corresponding to . Under a certain set of assumptions, this isosurface is optimal in the least squares sense. A full proof of this optimality is beyond the scope of this paper, but a sketch appears in appendix A.

Figure 2 illustrates the principle of combining unweighted signed distances for the simple case of two range surfaces sampled from the same direction. Note that the resulting isosurface would be the surface created by averaging the two range surfaces along the sensor's lines of sight. In general, however, weights are necessary to represent variations in certainty across the range surfaces. The choice of weights should be specific to the range scanning technology. For optical triangulation scanners, for example, Soucy [25] and Turk [30] make the weight depend on the dot product between each vertex normal and the viewing direction, reflecting greater uncertainty when the illumination is at grazing angles to the surface. Turk also argues that the range data at the boundaries of the mesh typically have greater uncertainty, requiring more down-weighting. We adopt these same weighting schemes for our optical triangulation range data.

 
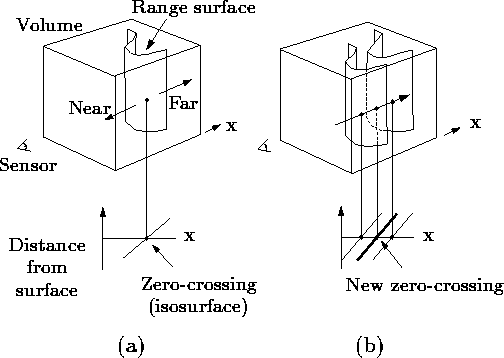
Figure 2: Unweighted signed distance functions in 3D. (a) A range sensor looking down the x-axis observes a range image, shown here as a reconstructed range surface. Following one line of sight down the x-axis, we can generate a signed distance function as shown. The zero crossing of this function is a point on the range surface. (b) The range sensor repeats the measurement, but noise in the range sensing process results in a slightly different range surface. In general, the second surface would interpenetrate the first, but we have shown it as an offset from the first surface for purposes of illustration. Following the same line of sight as before, we obtain another signed distance function. By summing these functions, we arrive at a cumulative function with a new zero crossing positioned midway between the original range measurements. 

Figure 3 illustrates the construction and usage of the signed distance and weight functions in 1D. In Figure 3a, the sensor is positioned at the origin looking down the +x axis and has taken two measurements, and . The signed distance profiles, and may extend indefinitely in either direction, but the weight functions, and , taper off behind the range points for reasons discussed below.

Figure 3b is the weighted combination of the two profiles. The combination rules are straightforward:

 

 

where, and are the signed distance and weight functions from the ith range image.

Expressed as an incremental calculation, the rules are:

 

 

where and are the cumulative signed distance and weight functions after integrating the ith range image.

In the special case of one dimension, the zero-crossing of the cumulative function is at a range, R given by:

i.e., a weighted combination of the acquired range values, which is what one would expect for a least squares minimization.

 
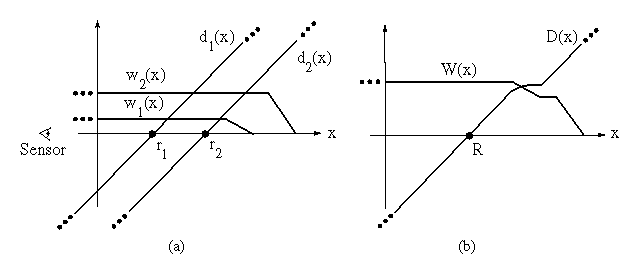
Figure 3: Signed distance and weight functions in one dimension. (a) The sensor looks down the x-axis and takes two measurements, and . and are the signed distance profiles, and and are the weight functions. In 1D, we might expect two sensor measurements to have the same weight magnitudes, but we have shown them to be of different magnitude here to illustrate how the profiles combine in the general case. (b) D(x) is a weighted combination of and , and W(x) is the sum of the weight functions. Given this formulation, the zero-crossing, R, becomes the weighted combination of and and represents our best guess of the location of the surface. In practice, we truncate the distance ramps and weights to the vicinity of the range points. 

In principle, the distance and weighting functions should extend indefinitely in either direction. However, to prevent surfaces on opposite sides of the object from interfering with each other, we force the weighting function to taper off behind the surface. There is a trade-off involved in choosing where the weight function tapers off. It should persist far enough behind the surface to ensure that all distance ramps will contribute in the vicinity of the final zero crossing, but, it should also be as narrow as possible to avoid influencing surfaces on the other side. To meet these requirements, we force the weights to fall off at a distance equal to half the maximum uncertainty interval of the range measurements. Similarly, the signed distance and weight functions need not extend far in front of the surface. Restricting the functions to the vicinity of the surface yields a more compact representation and reduces the computational expense of updating the volume.

In two and three dimensions, the range measurements correspond to curves or surfaces with weight functions, and the signed distance ramps have directions that are consistent with the primary directions of sensor uncertainty. The uncertainties that apply to range image integration include errors in alignment between meshes as well as errors inherent in the scanning technology. A number of algorithms for aligning sets of range images have been explored and shown to yield excellent results [11][30]. The remaining error lies in the scanner itself. For optical triangulation scanners, for example, this error has been shown to be ellipsoidal about the range points, with the major axis of the ellipse aligned with the lines of sight of the laser [13][24].

Figure 4 illustrates the two-dimensional case for a range curve derived from a single scan containing a row of range samples. In practice, we use a fixed point representation for the signed distance function, which bounds the values to lie between and as shown in the figure. The values of and must be negative and positive, respectively, as they are on opposite sides of a signed distance zero-crossing.

 
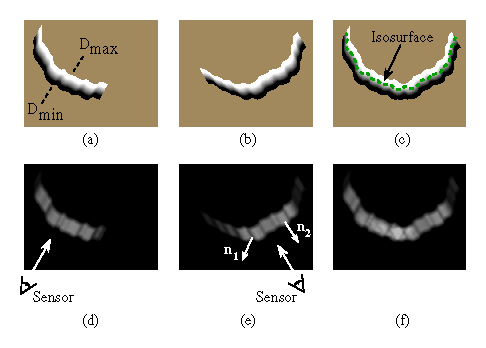
Figure 4: Combination of signed distance and weight functions in two dimensions. (a) and (d) are the signed distance and weight functions, respectively, generated for a range image viewed from the sensor line of sight shown in (d). The signed distance functions are chosen to vary between and , as shown in (a). The weighting falls off with increasing obliquity to the sensor and at the edges of the meshes as indicated by the darker regions in (e). The normals, and shown in (e), are oriented at a grazing angle and facing the sensor, respectively. Note how the weighting is lower (darker) for the grazing normal. (b) and (e) are the signed distance and weight functions for a range image of the same object taken at a 60 degree rotation. (c) is the signed distance function corresponding to the per voxel weighted combination of (a) and (b) constructed using equations 3 and 4. (f) is the sum of the weights at each voxel, . The dotted green curve in (c) is the isosurface that represents our current estimate of the shape of the object. 

For three dimensions, we can summarize the whole algorithm as follows. First, we set all voxel weights to zero, so that new data will overwrite the initial grid values. Next, we tessellate each range image by constructing triangles from nearest neighbors on the sampled lattice. We avoid tessellating over step discontinuities (cliffs in the range map) by discarding triangles with edge lengths that exceed a threshold. We must also compute a weight at each vertex as described above.

Once a range image has been converted to a triangle mesh with a weight at each vertex, we can update the voxel grid. The signed distance contribution is computed by casting a ray from the sensor through each voxel near the range surface and then intersecting it with the triangle mesh, as shown in figure 5. The weight is computed by linearly interpolating the weights stored at the intersection triangle's vertices. Having determined the signed distance and weight we can apply the update formulae described in equations 3 and 4.

 
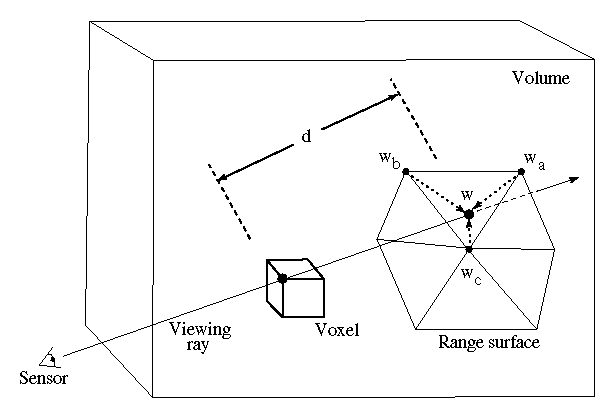
Figure 5: Sampling the range surface to update the volume. We compute the weight, w, and signed distance, d, needed to update the voxel by casting a ray from the sensor, through the voxel onto the range surface. We obtain the weight, w, by linearly interpolating the weights ( , , and ) stored at neighboring range vertices. Note that for a translating sensor (like our Cyberware scanner), the sensor point is different for each column of range points. 

At any point during the merging of the range images, we can extract the zero-crossing isosurface from the volumetric grid. We restrict this extraction procedure to skip samples with zero weight, generating triangles only in the regions of observed data. We will relax this restriction in the next section.