

Next: 5 Implementation
Up: A Volumetric Method
Previous: 3 Volumetric integration
The algorithm described in the previous section is designed to
reconstruct the observed portions of the surface. Unseen portions of
the surface will appear as holes in the reconstruction. While this
result is an accurate representation of the known surface, the holes
are esthetically unsatisfying and can present a stumbling block to
follow-on algorithms that expect continuous meshes. In
[17], for example, the authors describe a
method for parameterizing patches that entails generating evenly
spaced grid lines by walking across the edges of a mesh. Gaps in the
mesh prevent the algorithm from creating a fair parameterization. As
another example, rapid prototyping technologies such as
stereolithography typically require a ``watertight'' model in order to
construct a solid replica [7].
One option for filling holes is to operate on the reconstructed mesh.
If the regions of the mesh near each hole are very nearly planar, then
this approach works well. However, holes in the meshes can be (and
frequently are) highly non-planar and may even require connections
between unconnected components. Instead, we offer a hole filling
approach that operates on our volume, which contains more information
than the reconstructed mesh.
The key to our algorithm lies in classifying all points in the volume
as being in one of three states: unseen, empty, or near the surface.
Holes in the surface are indicated by frontiers between unseen regions
and empty regions (see Figure 6). Surfaces placed
at these frontiers offer a plausible way to plug these holes (dotted
in Figure 6). Obtaining this classification and
generating these hole fillers leads to a straightforward extension of
the algorithm described in the previous section:
-
Initialize the voxel space to the ``unseen'' state.
-
Update the voxels near the surface as described in the previous
section. As before, these voxels take on continuous signed distance
and weight values.
-
Follow the lines of sight back from the observed surface and mark the
corresponding voxels as ``empty''. We refer to this step as
space carving.
-
Perform an isosurface extraction at the zero-crossing of the signed
distance function. Additionally, extract a surface between regions
seen to be empty and regions that remain unseen.
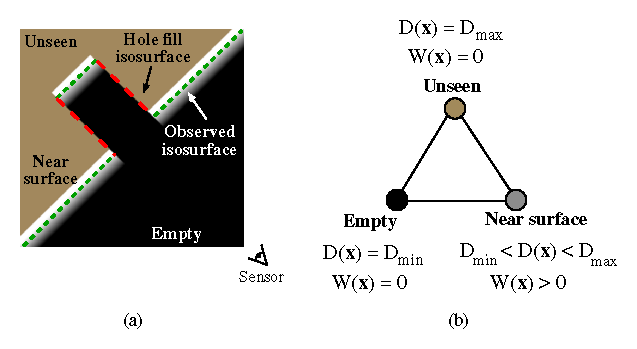
Figure 6: Volumetric grid with space carving and hole filling. (a) The regions
in front of the surface are seen as empty, regions in the vicinity of
the surface ramp through the zero-crossing, while regions behind
remain unseen. The green (dashed) segments are the isosurfaces
generated near the observed surface, while the red (dotted) segments
are hole fillers, generated by tessellating over the transition from
empty to unseen. In (b), we identify the three extremal voxel states
with their corresponding function values.
In practice, we represent the unseen and empty states using the
function and weight fields stored on the voxel lattice. We represent
the unseen state with the function values 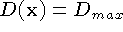 ,
,
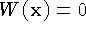 and the empty state with the function values
and the empty state with the function values 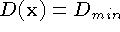 ,
, 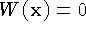 , as shown in
Figure 6b. The key advantage of this representation
is that we can use the same isosurface extraction algorithm we used in
the previous section without the restriction on interpolating voxels
of zero weight. This extraction finds both the signed distance and
hole fill isosurfaces and connects them naturally where they meet,
i.e., at the corners in Figure 6a where the dotted
red line meets the dashed green line. Note that the triangles that
arise from interpolations across voxels of zero weight are distinct
from the others: they are hole fillers. We take advantage of this
distinction when smoothing surfaces as described below.
, as shown in
Figure 6b. The key advantage of this representation
is that we can use the same isosurface extraction algorithm we used in
the previous section without the restriction on interpolating voxels
of zero weight. This extraction finds both the signed distance and
hole fill isosurfaces and connects them naturally where they meet,
i.e., at the corners in Figure 6a where the dotted
red line meets the dashed green line. Note that the triangles that
arise from interpolations across voxels of zero weight are distinct
from the others: they are hole fillers. We take advantage of this
distinction when smoothing surfaces as described below.
Figure 6 illustrates the method for a single range
image, and provides a diagram for the three-state classification
scheme. The hole filler isosurfaces are ``false'' in that they are
not representative of the observed surface, but they do derive from
observed data. In particular, they correspond to a boundary that
confines where the surface could plausibly exist. In practice, we
find that many of these hole filler surfaces are generated in crevices
that are hard for the sensor to reach.
Because the transition between unseen and empty is discontinuous and
hole fill triangles are generated as an isosurface between these
binary states, with no smooth transition, we generally observe
aliasing artifacts in these areas. These artifacts can be eliminated
by prefiltering the transition region before sampling on the voxel
lattice using straightforward methods such as analytic filtering or
super-sampling and averaging down. In practice, we have obtained
satisfactory results by applying another technique: post-filtering the
mesh after reconstruction using weighted averages of nearest vertex
neighbors as described in
[29]. The effect of this filtering step is
to blur the hole fill surface. Since we know which triangles
correspond to hole fillers, we need only concentrate the surface
filtering on the these portions of the mesh. This localized filtering
preserves the detail in the observed surface reconstruction. To
achieve a smooth blend between filtered hole fill vertices and the
neighboring ``real'' surface, we allow the filter weights to extend
beyond and taper off into the vicinity of the hole fill boundaries.
We have just seen how ``space carving'' is a useful operation: it
tells us much about the structure of free space, allowing us to fill
holes in an intelligent way. However, our algorithm only carves back
from observed surfaces. There are numerous situations where more
carving would be useful. For example, the interior walls of a hollow
cylinder may elude digitization, but by seeing through the hollow
portion of the cylinder to a surface placed behind it, we can better
approximate its geometry. We can extend the carving paradigm to cover
these situations by placing such a backdrop behind the surfaces being
scanned. By placing the backdrop outside of the voxel grid, we
utilize it purely for carving space without introducing its geometry
into the model.


Next: 5 Implementation
Up: A Volumetric Method
Previous: 3 Volumetric integration
