|
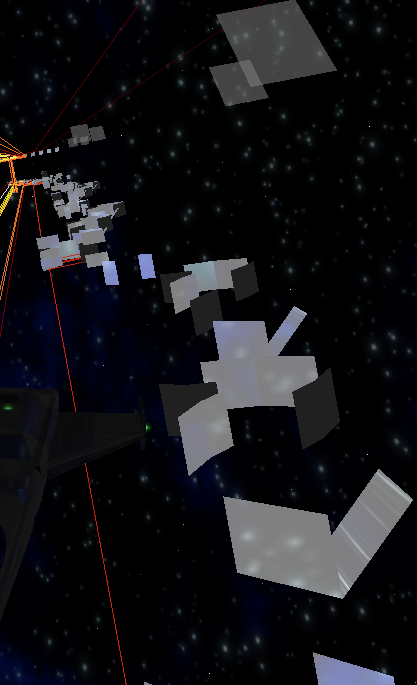
What is the Raytrix |
 |
The Raytrix
With Monte Carlo techniques, path tracing, and other time consuming techniques for finding rays that origin from a light source, ray tracing begs the question: how complex is it to find the destination of a ray given its source, or vice versa.
Reif, Tygar and Yoshida show that it is not only time consuming to determine the destination of a ray from its input location, but that it is undecidable. They accomplish this proof by using a ray fired into a specific scene to simulate the universal Turing machine.
The idea is as follows:
The entire computers memory is saved as two stacks, each saved in the fraction of the ray's X and Y position respectively. If a ray were at x=1011010111.11001 y=111.1011 (in decimal x=727.78125 y=7.6875) then the X stack would have 1100100000.... and the Y stack would have 1011000000000.... on it.
Given unlimited precision, this can easily hold the whole Turing machine's tape, with the head pointing to the gap between the X and the Y stacks. The stack may be manipulated as follows:
There are 3 basic commands:
- if(top) redirect beam:
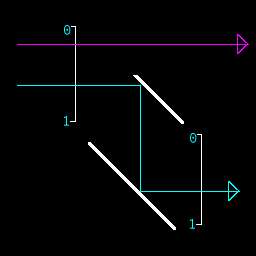
- add k to stack:
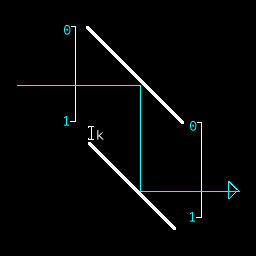
- push (or pop) stack: (multiply or divide ray position by 2) This functions by having 2 parabolas of different sizes which share a focus.
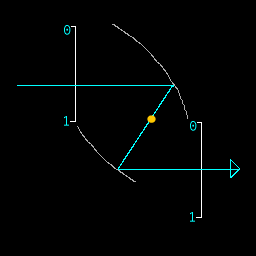
Each operation may be chained by mirrors and each operation may be performed on either the X or Y position independently. Thus the machine is a Turing machine.
|
Nondeterminism
However, the machine has another powerful function that was not addressed in the paper: It has the ability to act as a nondeterministic Turing machine by using partially transmissive surfaces (like glass).
assuming an input with the top bit off (binary representation 101110101011.011101101 first digit after . is zero) The fork device shown below can split the beam and allow two beams to continue through the entire machine.
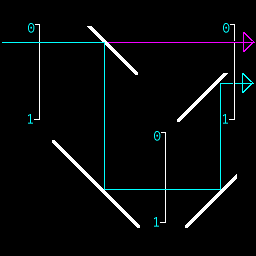
The Fork Instruction operates by using a partially reflective surface to bounce the light perpendicular, then bounces it around and adds .5 on the way. That way the top most bit will end up with both zero and one. After the fork instruction another push may be executed, and so forth to fill up an arbitrary number of bits with both zero and one values.
Here is an example of a number of fork commands being chained to result in 16 rays with the first four bits in both x and y being set to all possibilities.

(Image Height Stretched to 2x)
In this way it is possible to solve problems in NP with only polynomial bounces per ray, resulting in a total polynomial number of bounces to solve the problem.
So it became my goal to write a 3sat solver that used only polynomial number of bounces
|
Compiler Tool-chain
To write a program with the complexity of 3-sat some assistance from a compiler is in order: manually placing the mirrors one by one would be error prone and tedious.
Instead I designed a compiler to do this for me. The entire tool-chain was written in the D programming language, a language still in alpha testing and undergoing a lot of flux--however also a clean high level language with careful typing rules and templates (both a requisite for a large project).
I began with writing the simulator: i.e. the ray-tracer itself. The reason I could not use PBRT is that the entire memory was stored as a single number; therefore a float would not be sufficient to hold this memory--and I would have to refrain from doing approximations like square roots and actually calculate the exact answers. I started with an alpha-version D BigInteger class and built upon it a templatized Big Rational, that allowed division, mult, add, sub, and even sqrt if the fraction was square. On top of this I built a template class for vector types with the exact interface that Cg has (it turns out that D is a superset of Cg's functionality!). So I ended up using rational3 vectors for all my computation. Then I wrote a ray-tracer that could intersect rays with axis-aligned parabolas and arbitrary quads. The interface was the same as PBRT with the DifferentialGeometry class returning a normal to be reflected over and a material property BSDF. I wrote part of a uniform grid implementation, but decided it would be best to wait until things were actually going slowly than to waste time now optimizing if necessary.
With the test system in place, I could fork rays, multiply them, add them, and build conditionals. I wrote little assembly statements by grouping together mirrors into 3x4x2 blocks to perform such tasks. All mirrors had closed edges, meaning that sometimes extra space was necessary to avoid edge cases failing.
I ended up with 8 commands that could each produce part of a scene file:
noop
kill (black surface destroys ray)
loop (reflect beam up and redirect to start of program)
invert (flop top bit on either x or y)
mod5 (set top bit to zero)
agetsb (set top bit of one stack to top bit of the other)
if (if the top bit of one stack is one redirect to another codepath)
fork (sets top bit to both zero and one and doubles simulated # of rays)
plusgets (adds a bit pattern to the stack)
mulgets (divide or multiply the stack by a value)
|
I combined these very low level commands into more useful commands that could be chained together by some C++ code:
< var> indicates to which stack the instruction will apply
< index> indicates to which bit in the stack the instruction will apply
If (< var>, < index> ); Checks if the indexth bit of stack var is set. if so execute code until EndIf
IfPop (< var>, < index> ); Checks if the indexth bit of stack var is set and pops it. If so execute code until EndIf
EndIf(); Loops to the beginning of the program
Pop(< var > ); pops value from the < var> stack
PopXX(< var > , num); pops num values from < var> stack
void PushXX(< var >, value, nbits); pushes nbits of bit pattern contained in value onto stack
Fork(< var >, < index> ); Sets indexth bit to both zero and one
Exit(); Terminate ray with failure
|
With these eight commands that were made of the previous nine, I was able to program 3-sat in assembly.
Each of the instructions printed itself to a scene file with the appropriate location determined by the layout algorithm below, and each instruction also wrote itself out as a D array command, since D arrays had all the functionality of stacks. So I could test the output program as either a native x86 executable or as a raytraced (interpreted) scene file. This helped me write 3-sat
I had to write a layout algorithm that would lay out these carefully pieced together commands into a larger map. I accomplished this by keeping the invariant that each piece would be farther along in z, and potentially father along in x, but never decreasing in x nor increasing or decreasing in y. With this invariant, layout became trivial: I would layout the next item in z that was greatest in x and all of its children first, then I would layout the item lesser in x at the farthest unused z value. This would ensure an O(n) time layout of the building blocks of the programs. Since loops only looped to the beginning it was trivial; however, I had a mechanism for making looping constructs jump anywhere, I just did not implement it. This would have involved pushing the address of the desired instruction and then magnifying the ray until it hit the exact destination instruction location.
My first successful program was the loop x=y, where x's value would be copied to y.
The result of the run of the program is illustrated below: the ray is dyed by time, the darker, the more intersections it had to perform. The output is indicated with "END".
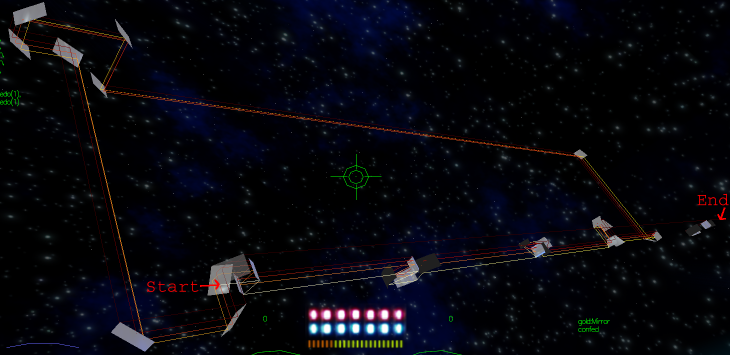
It literally loops around 10 times, and it really brings to light why a loop is so named.
|
|